Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:
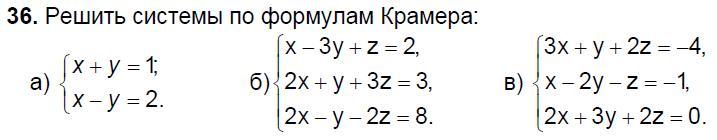
Ответы
Автор ответа:
2
Ответ:
36.
а)
б)
в)
Приложения:



Похожие вопросы
Предмет: Русский язык,
автор: 11Аполинария11
Предмет: Русский язык,
автор: Виктория1950
Предмет: Русский язык,
автор: НикаЭванс
Предмет: Алгебра,
автор: dantv1058