Question

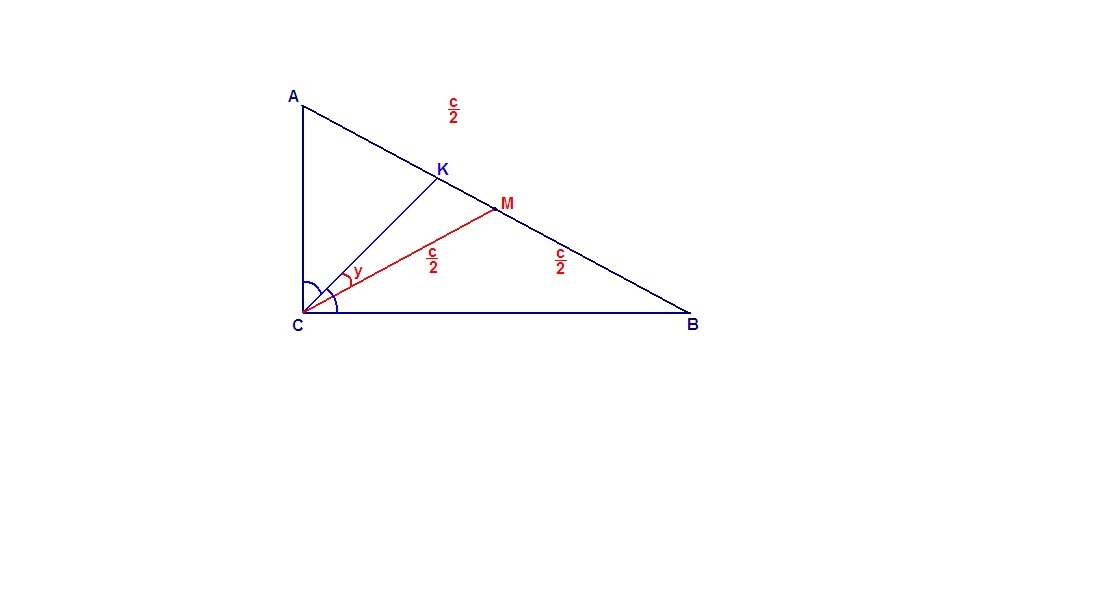
Угол между медианой и биссектрисой,проведенной из вершины прямого угла прямоугольного треугольника равен y,а гипотенуза равна с.найти S. треугольника

Answer 1

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине:

CM = AM = BM = c/2

∠КСВ = 90° / 2 = 45°, так как СК биссектриса, тогда

∠МСВ = 45° - у.

ΔМСВ равнобедренный, значит

∠МВС = ∠МСВ = 45° - у.

Найдем угол СМВ:

∠СМВ = 180° - (∠МВС + ∠МСВ) = 180° - (90° - 2у) = 90° + 2у

Площадь треугольника СМВ:

Scmb = 1/2 MC · MB · sin∠CMB

Scmb = 1/2 · c/2 · c/2 · sin(90° - 2y) = c²/8 · cos(2y),

т.к. sin(90° - α) = cosα

Медиана делит треугольник на два равновеликих (равных по площади), поэтому

Sabc = 2Scmb = c²/4 · cos(2y)