Question

Срочно решите задачу даю 90 баллов. Меньшая диагональ правильного шестиугольника равна 9√3 см. Найдите периметр шестиугольника.

Answer 1

Ответ:
54см

Решение:
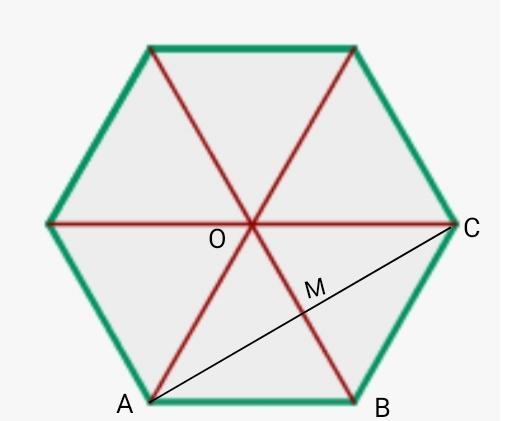
АС=9√3см
АМ=АС/2=9√3/2=4,5√3 см.
АМ- высота равностороннего треугольника ∆АВО.
Из формулы нахождения высоты равностороннего треугольника:
h=a√3/2, где а-сторона треугольника.
АМ=АВ√3/2, найдем АВ.
АВ=2*АМ/√3=2*4,5√3/√3=9см.
Р=6*АВ=6*9=54см

Answer 2

Ответ:

Объяснение:

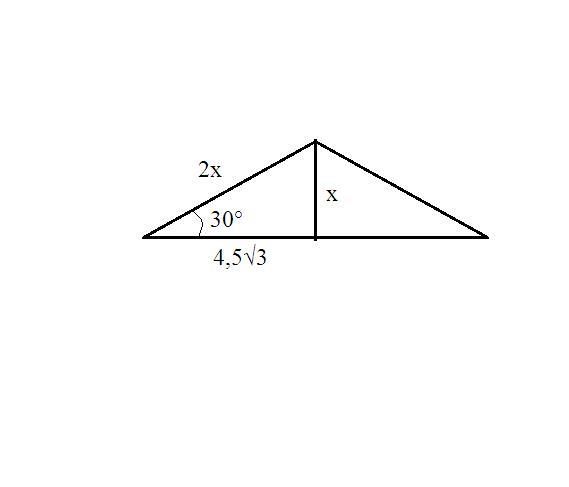
Углы  правильного шестиугольника равны 120°.

Две соседние стороны шестиугольника и его меньшая диагональ образуют равнобедренный треугольник с углами при основании 30°.

Проводим высоту к основанию. Образовавшийся треугольник прямоугольный. Катет против угла 30° - х см, второй катет - 9√3/2=4,5√3 см, гипотенуза (половина стороны шестиугольника) 2х см;

по т. Пифагора:

4х²=(4,5√3)²+х²

3х²=3*4,5²

х=4,5 см - половина длины стороны шестиугольника;

4,5*2=9 см - длина стороны;

9*6=54 см - периметр.