Предмет: Геометрия,
автор: ghhbbbbb
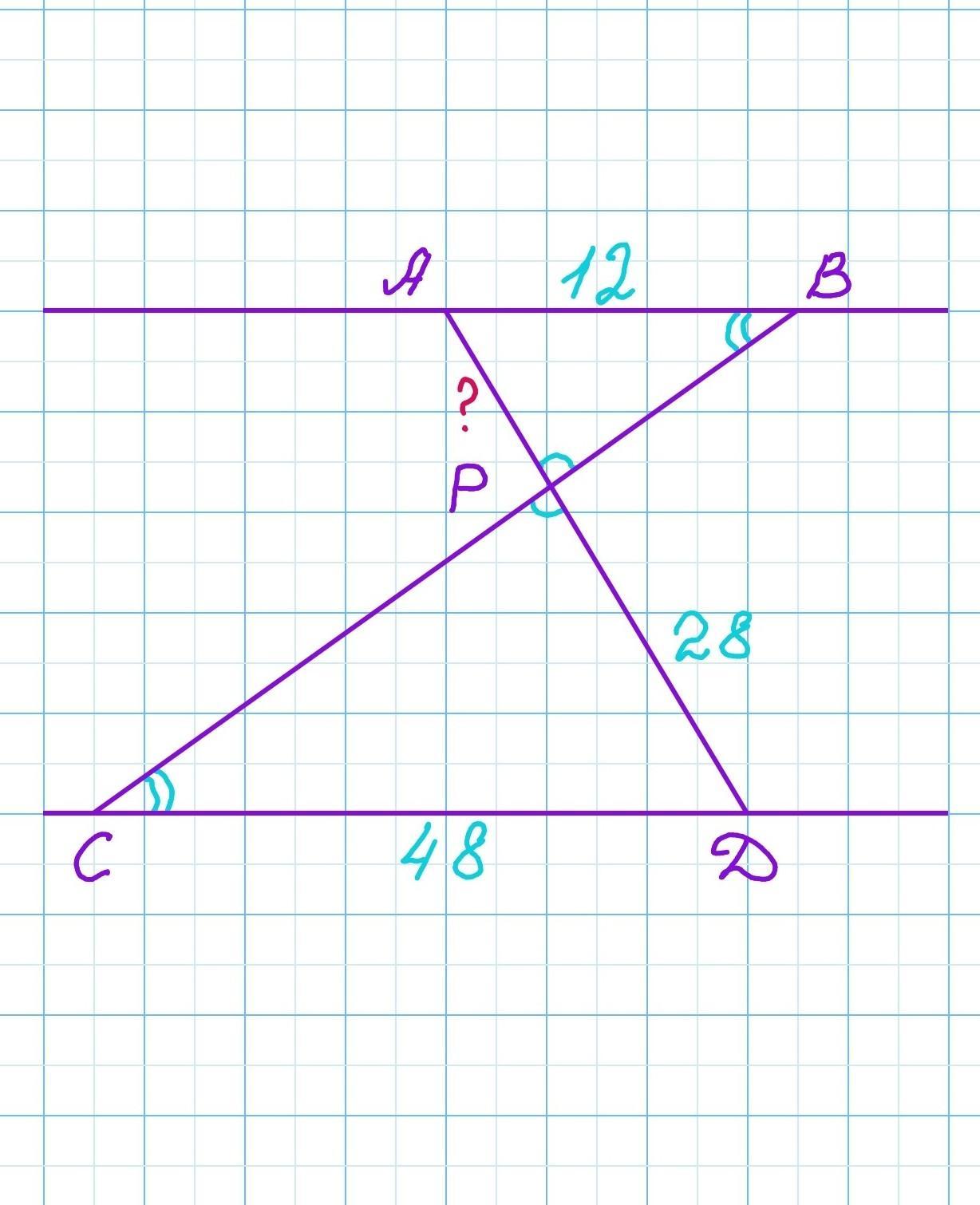
Отрезки AB и CD лежат на параллельных прямых, а отрезки AD и BC пересекаются в точке P. Известно, что PD=28, AB=12, DC=48.
Найдите AP и AD.
sergey18110:
ты решил?
Ответы
Автор ответа:
6
Ответ:
AP=7 ед,
AD=35 ед
Объяснение:
Отрезки AB и CD лежат на параллельных прямых, а отрезки AD и BC пересекаются в точке P. Известно, что PD=28, AB=12, DC=48.
НАЙДЁМ AP и AD.
Рассмотрим △ABP и △DCP.
∠ABP=∠DCP - как внутренние накрест лежащие углы при параллельных прямых AB и DC и секущей BC.
∠BPA=∠CPD - как вертикальные.
Следовательно треугольник ABP подобен треугольнику DCP по двум углам.
Значит,
АР = 7 ед
AD=AP+DP=7+28=35 ед
#SPJ1
Приложения:
можешь пожалуйста решить еще одну задачу?
Похожие вопросы
Предмет: Русский язык,
автор: Stasy051
Предмет: Русский язык,
автор: Dautovi2016
Предмет: Английский язык,
автор: Nikita52670
Предмет: Литература,
автор: stefa0706
Предмет: Математика,
автор: VBIF1124