Предмет: Алгебра,
автор: MaryAndryway
У меня возникает вопрос при решении этой задачи и одна из загвоздок в том,что надо её решить квадратным уравнением.Помогите пожалуйста.
Приложения:
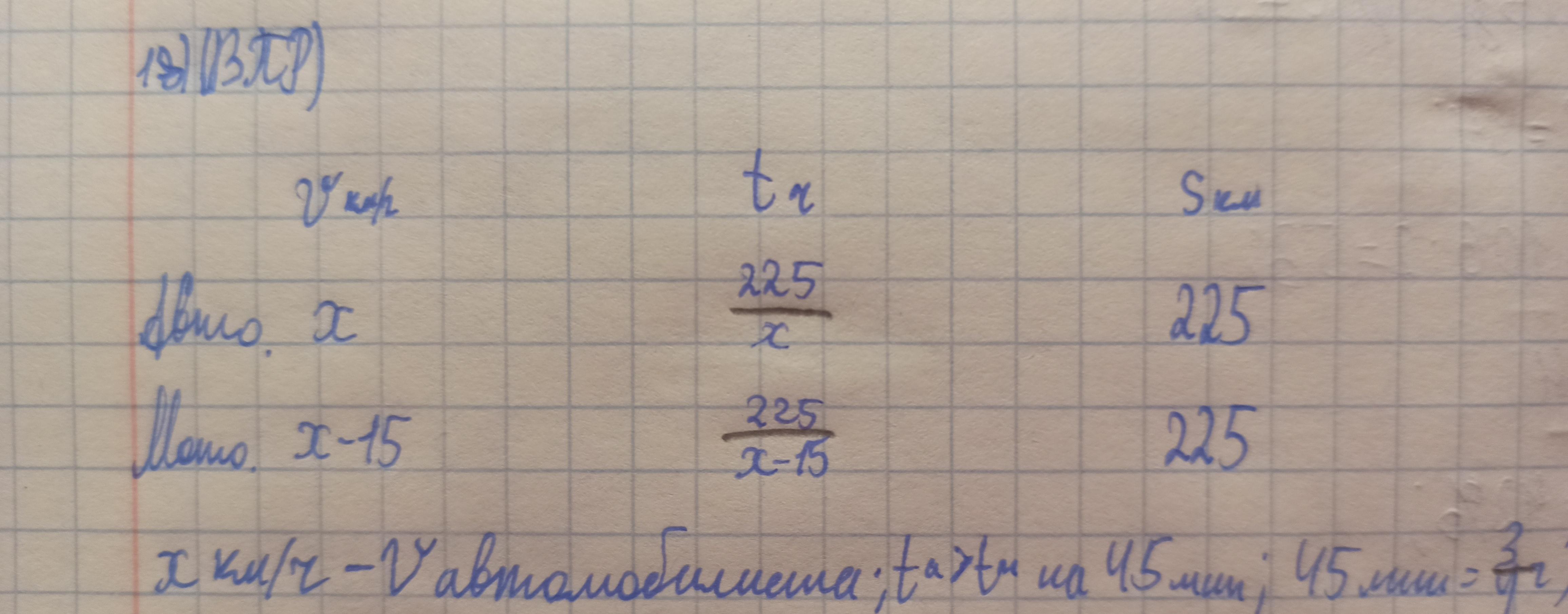
SklMatt:
что нужно найти, скорость? чью?
надо найти скорость автомобилиста
скорость автомобилиста - 75, а мотоцикла - 60
Ответы
Автор ответа:
1
Объяснение:
(ты ошибся: ta < tm на 45минут, т.к у автомобиля больше скорость и ее время не может быть больше)
Пусть Va будет х
Тогда Vm будет х-15
По условию S=225
т.к ta < tm на 45 мин, то можем из большего значения вычесть меньшее и приравнять к 45минутам - 3/4ч
Составим и решим уравнение:
tm-ta=3/4
Найдем ОДЗ:
1)х-15≠0
х≠15
2)х≠0
Приводим к общему знаменателю
Дробь равна нулю, когда числитель равен нулю, поэтому приравняем числитель к нулю
умножим на -1
разделим на 3
x2 не удовлетворяет условию, т.к скорость не может быть отрицательной, поэтому скорость автомобиля равна 75км/ч
(непонятно, что нужно найти)
Vm=x-15=75-15=60
Ответ:75;60
Похожие вопросы
Предмет: Окружающий мир,
автор: лео63
Предмет: Окружающий мир,
автор: ksyusa19
Предмет: Русский язык,
автор: goregliadaniut
Предмет: Математика,
автор: kai7824
Предмет: Алгебра,
автор: larsab