решите уравнение
..
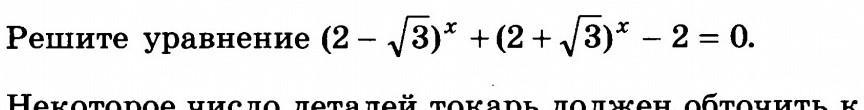
Ответы
Ответ:
х=0.
Объяснение:
Подумаем. Значения показательной функции всегда положительны.
То есть, выражения "(2-√3)^х" и "(2+√3)^х" – обязательно положительны. Далее. Сумма двух положительных выражений равна положительному выражению. Теперь, помним, что (2-√3)^х + (2+√3)^х – результат положительный. Мы подходим к финалу. В каком случае при вычитании положительного выражения от отрицательного выходит ноль? Когда перовое слагаемое равно второму, но с противоположным знаком. Формулировка мыслей не мой конёк... То есть, к чему я веду. Например. 5-5=0; 2-2=0 и т.д. Как можно представить 2? Как 1+1. А как из выражений "(2-√3)^х" и "(2+√3)^х" получить единицы? Есть прекрасное свойство: а^0=1. Итак. Подберём корень уравнения.
(2-√3)^0+(2+√3)^0-2=0.
Любое число, кроме нуля, в нулевой степени =1. Значит, 1 + 1 - 2 = 0. Тогда, 2-2=0; и наконец 0=0. Ура! Мы выяснили, что число 0 – корень уравнения. Других нет.
___________________________
Алгебраического решения найти я не смог. Метод "тыка".