Помогите пожалуйста!!! Каноническое уравнение прямой. Как решать???
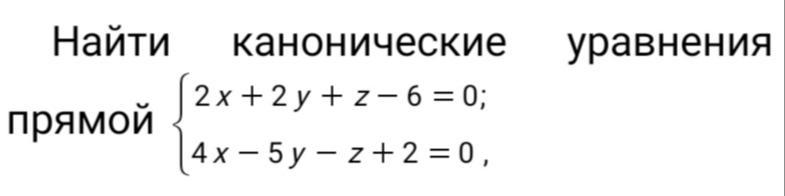
Ответы
Записать канонические уравнения прямой d:{█(2x+2y+z-6=0@4x-5y-z+2=0)┤
Решение: Чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей….
1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? Так как линия пересекает плоскость хОу, то в этой точке координата z = 0.
Поэтому в системе уравнений нужно обнулить координату z.
Пусть z = 0, тогда получаем систему двух линейных уравнений с двумя неизвестными: . {█(2x+2y-6=0@4x-5y+2=0)┤
Решаем систему: {█(2x+2y-6=0 |x(5)=10x+10y-30=0@4x-5y+2=0 |x(2)=8x-10y+4=0)┤
Почленно складываем уравнения и находим решение системы:
18x – 26 = 0,
x = 26/18 = 13/9,
y = (6 - 2x)/2 = = (6 – (2*13/9))/2 = (54 – 26)/18 = 28/18 = 14/9.
Таким образом, точка M((13/9); (14/9); 0) принадлежит данной прямой.
2) Как найти направляющий вектор прямой?
Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей. А если , то вектор «p» найдём как векторное произведение векторов нормали: .
Из уравнений плоскостей {█(2x+2y+z-6=0@4x-5y-z+2=0)┤ снимаем их векторы нормали:
n1(2; 2 1), n2(4; -5; -1).
И находим направляющий вектор p прямой d, перпендикулярный двум заданным с помощью векторного произведения.
I j k| I j
2 2 1| 2 2
4 -5 -1| 4 -5 = -2i + 4j - 10k + 2j + 5i – 8k = 3i + 6j -18k.
Вектор p = (3; 6; -18).
3) Составим канонические уравнения прямой по точке M((13/9); (14/9); 0) и направляющему вектору : p = (3; 6; -18).
(x-13/9)/3=(y-14/9)/6=z/(-18)
Ответ: d:(x-13/9)/3=(y-14/9)/6=z/(-18)
На практике можно пользоваться готовой формулой: если прямая задана пересечением двух плоскостей , то вектор является направляющим вектором данной прямой.
Ответ с более качественным форматированием дан во вложении.