Предмет: Математика,
автор: germannikita06
Решить уравнение
2 sin2 x - sin xcos x - 3 cos2x = 0
40 балллов
Приложения:
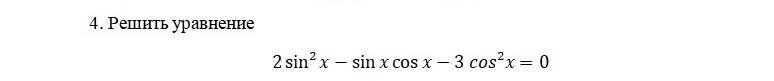
Ответы
Автор ответа:
0
2sin²(x) - sin(x)cos(x) - 3cos²(x) = 0
• Данное уравнение является однородным II типа, поэтому можем поделить обе части на cos²(x), причём cos(x) ≠ 0, ⇒ x ≠ π/2 + πn, n ∈ ℤ
• После деления, получаем:
2tg²(x) - tg(x) - 3 = 0
• Пусть tg(x) = t, тогда:
2t - t - 3 = 0
(a = 2, b = -1, c = -3)
D = b² - 4ac
D = (-1)² - 4 • 2 • (-3) = 1 + 24 = 25 = 5²
t = (-b ± √D)/2a
t₁ = (-(-1) + 5)/2 • 2 = 6/4 = 3/2 = 1,5
t₂ (-(-1) - 5)/2 • 2 = -4/4 = -1
• Система:
[ tg(x) = 1,5
[ tg(x) = -1
[ x₁ = arctg(1,5) + πn, n ∈ ℤ
[ x₂ = -π/4 + πn, n ∈ ℤ
Ответ: x₁ = arctg(1,5) + πn, n ∈ ℤ
x₂ = -π/4 + πn, n ∈ ℤ
Похожие вопросы
Предмет: Русский язык,
автор: yasyapotapova7
Предмет: Українська мова,
автор: Макс110111
Предмет: Английский язык,
автор: 17111980
Предмет: Алгебра,
автор: thiix
Предмет: Українська мова,
автор: RitaBro