Предмет: Геометрия,
автор: AppleGameplays5
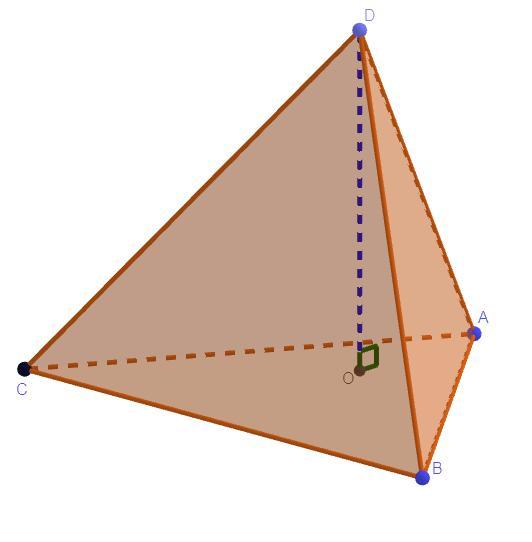
В правильной треугольной пирамиде DABC с вершиной D биссектрисы треугольника ABC пересекаются в точке O. Площадь треугольника ABC равна 2, объём пирамиды равен 6. Найдите длину отрезка DO.
Simba2017:
V=6=Sh/3=2h/3; h=18/2=9
Ответы
Автор ответа:
1
Ответ:
OD = 9
Объяснение:
Основанием правильной треугольной пирамиды является правильный треугольник. В точку O пересечения биссектрис проектируется точка D согласно теореме, тогда OD - высота пирамиды DABC.
⇒
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: AzizD
Предмет: Қазақ тiлi,
автор: vovagerasimov1
Предмет: Қазақ тiлi,
автор: dil2002naz
Предмет: Математика,
автор: Kraki
Предмет: Химия,
автор: forzer221