Предмет: Алгебра,
автор: undina77
Найти неопределенные интегралы методом замены переменной
Приложения:
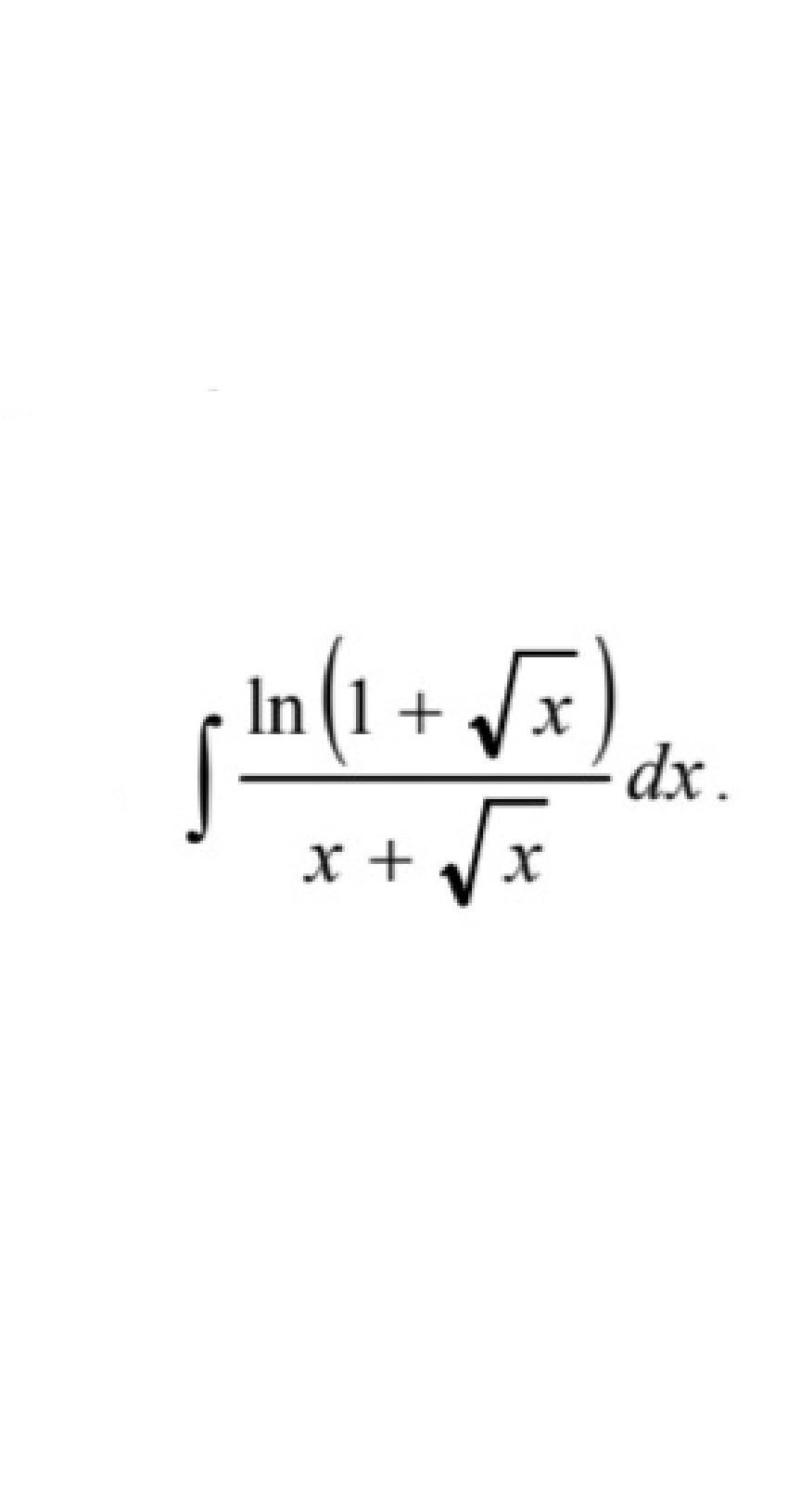
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Українська мова,
автор: lesyash82
Предмет: Русский язык,
автор: марыся3
Предмет: Русский язык,
автор: Jenya1111111
Предмет: Русский язык,
автор: Оляматематик
Предмет: Математика,
автор: kalotototoroo