Question

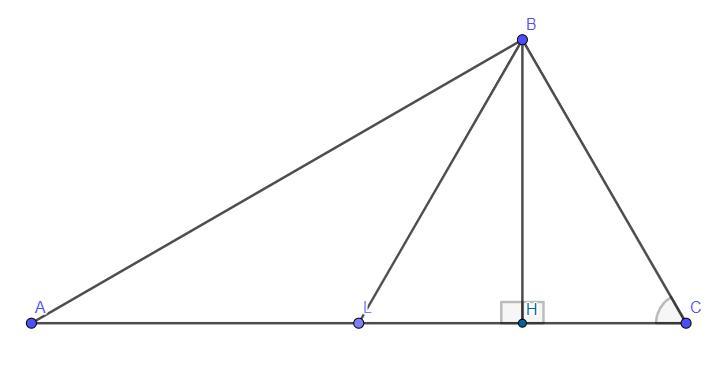
В треугольнике АВС, BL - медиана, проведенная к основанию, а BH - высота, отпущенная на основание. Известно, что АС=16, HC=4 и угол ACB=60°. Найти угол ALB.​

Answer 1

Ответ:

∠ALB = 120°.

Объяснение:

Дано: BL - медиана, BH⊥AC,BH - высота ,∠ACB = 60°,  AC = 16, HC = 4

Найти:  ∠ALB - ?

Решение: Так как BL - медиана по условию, то AL = LC = AC : 2 = 16 : 2 = 8.

LC = LH + HC ⇒ LH = LC - HC = 8 - 4 = 4.Треугольник ΔLHB = ΔCHB по первому признаку равенства треугольников так как, LH = HC = 4см, ∠LHB = ∠CHB = 90° так как по условию BH - высота, а сторона BH - общая для треугольников. Так как треугольник ΔLHB = ΔCHB, то соответствующие элементы треугольников равны, тогда ∠ACB = ∠BLC и ∠BLC = 60°.

Угол ∠ALB и ∠BLC - смежные, по свойству смежных углов их сумма 180°, тогда ∠ALB + ∠BLC = 180° ⇒ ∠ALB = 180° - ∠BLC = 180° - 60° = 120°.

Answer 2

Дано:

$зABC$ (см. рис), $BL$ - медиана, $BH$ - высота, $AC=16$, $HC=4$, ∠$ACB=60а$.

Найти:

∠$ALB-?$

Решение:

в $зABC$:

1) $BL$ - медиана, то $LC=\frac{1}{2} AC=\frac{1}{2} *16=8$

в $зLBC$:

2) $LC=8$, $HC=4$ ⇒ $LH=LC-HC=8-4=4$.

3) $LH=HC$ ⇒ $BH$ - медиана. Так как $BH$ ещё является и высотой, то она также и биссектриса, а значит $зLBC$ - равнобедренный, отсюда ∠$BLC=$∠$BCL=60а$.

4) ∠$ALB$ и ∠$BLC$ - смежные, а значит ∠$ALB=180а-$∠$BLC=180а-60а=120а$.

Ответ: ∠$ALB=120а$.