Предмет: Геометрия,
автор: Человеквеквеквеквее
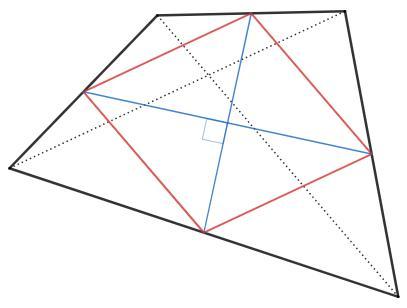
Найдите площадь выпуклого четырехугольника с равными диагоналями, если отрезки, соединяющие середины его противоположных сторон, равны 14 и 8.
Ответы
Автор ответа:
2
Соединим середины сторон четырехугольника.
Полученные отрезки параллельны диагоналям и равны их половинам, так как являются средними линиями в соответствующих треугольниках.
Отрезки образуют параллелограмм Вариньона.
Площадь четырехугольника Sч =1/2 d₁d₂ sinф
Угол ф между диагоналями четырехугольника равен углу между сторонами пар-ма Вариньона (т.к. они параллельны).
Площадь пар-ма Вариньона Sв =d₁/2 *d₂/2 *sinф =1/2 Sч
Итак, площадь пар-ма Вариньона равна половине площади четырехугольника.
В данном четырехугольнике диагонали равны, следовательно стороны пар-ма Вариньона равны и он является ромбом.
Диагонали ромба перпендикулярны, sin90=1.
Sч =2 Sв =2 *1/2 *14*8 =112
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Darinka19991
Предмет: Математика,
автор: allaosipenko
Предмет: Алгебра,
автор: Darinka19991
Предмет: Обществознание,
автор: romanostrovskii8
Предмет: Математика,
автор: Tralty