Предмет: Алгебра,
автор: Аноним
алгебра алгебра пожалуйста помогите
Приложения:

Ответы
Автор ответа:
1
Ответ:
Объяснение:
1.
Функция f(x) является непрерывной в точке x₀ , если её предел слева равен пределу справа и совпадает со значением функции в точке x₀:
Функция f(x) является непрерывной в точке x₀=2. (график№1).
2.
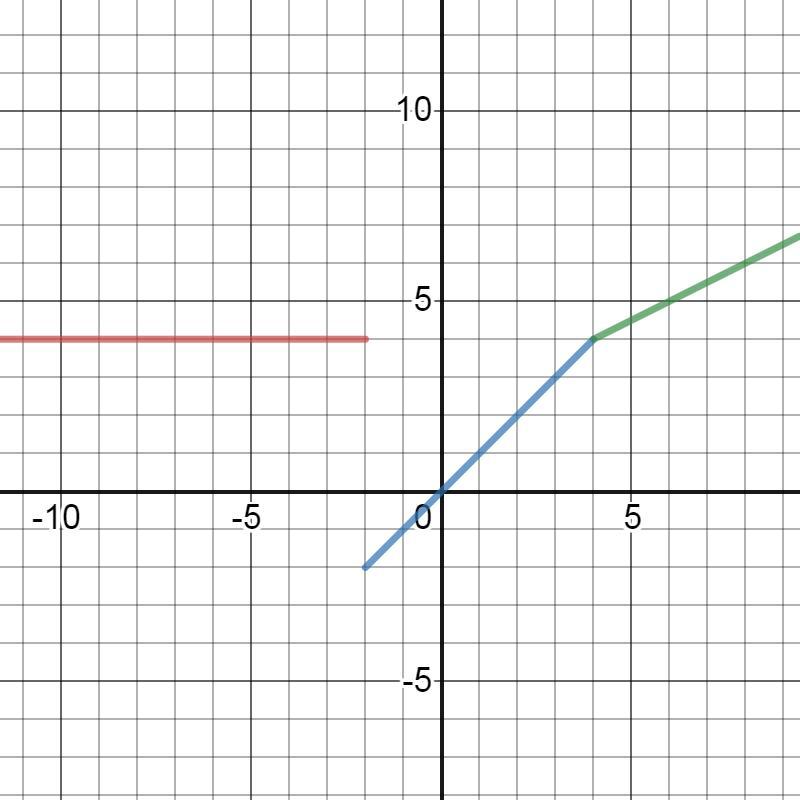
Функция f(x) является непрерывной в точке x₀ , если её предел слева равен пределу справа и совпадает со значением функции в точке x₀:
x₀=-2.
Таким образом, в точке х₀ =-2 определён неустранимый разрыв первого рода (скачок).
x₀'=4.
В точке х₀ = –4 заданная кусочная функция непрерывна (график №2).
Приложения:

Похожие вопросы
Предмет: Математика,
автор: tankist00127
Предмет: Алгебра,
автор: dases
Предмет: Английский язык,
автор: elimis
Предмет: Химия,
автор: seidametmustafa
Предмет: Обществознание,
автор: bearthis905