Предмет: Математика,
автор: mishax9
Интегралы
Нужна помощь...
Приложения:

Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
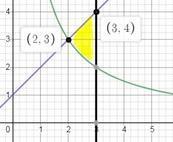
y₁ = 1+x; y₂=6/x; x = 3
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: denkiber
Предмет: Математика,
автор: dimas20141
Предмет: Математика,
автор: irinalysyh79
Предмет: Физика,
автор: малой51