Предмет: Алгебра,
автор: Iamnorman
Квадратичная функция вида y = ax² + bx + c, a ≠ 0 и ее график и свойства. Урок 1
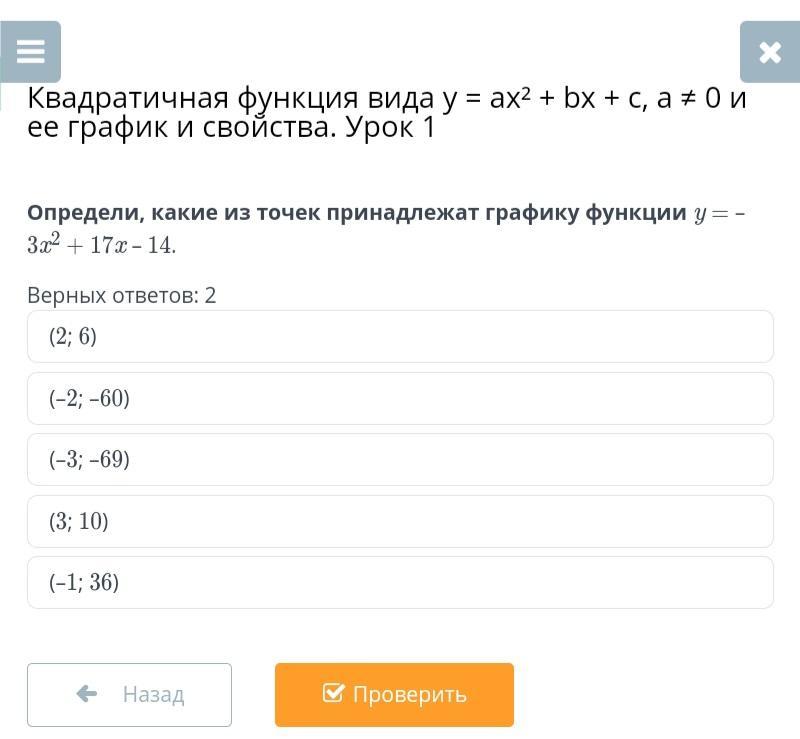
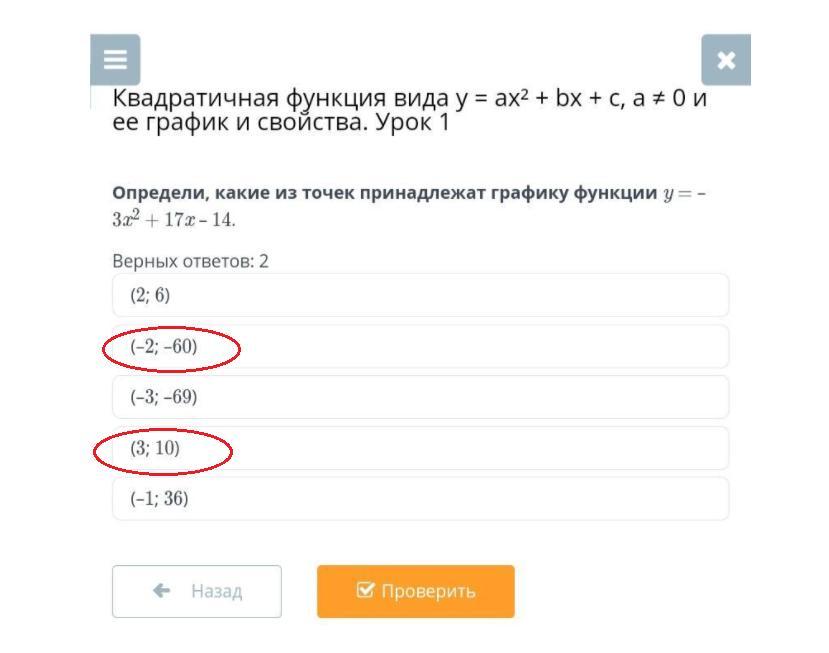
Определи, какие из точек принадлежат графику функции y = –3x2 + 17x – 14.
Приложения:
VlAdIsLaV857:
Лучший, спасибо!!!
ГЕРОЙ
спасибо огромноееееееееееее
Спасибо большое
спасибо
Я смотрю у нас тут фанаты Обещанного Неверленда))
И кстати спасибо за ответы)
Есть такое
Не за что
СПС
Ответы
Автор ответа:
4
Ответ:
(-2; -60) и (3; 10).
Объяснение:
Для того чтобы определить принадлежит ли точка графику функции, надо подставить координаты данных точек в уравнение. Если получим верное числовое равенство, то точка принадлежит графику.
Равенство неверно. Значит, точка (2; 6) не принадлежит графику
Равенство верно. Значит, точка (-2; -60) принадлежит графику.
Равенство неверно. Значит, точка (-3; -69) не принадлежит графику
Равенство верно. Значит, точка (3; 10) принадлежит графику.
Равенство неверно. Значит, точка (-1; 36) не принадлежит графику
Приложения:
Похожие вопросы
Предмет: Химия,
автор: Lisf
Предмет: Математика,
автор: dzgoevalena
Предмет: Математика,
автор: Montolon328
Предмет: Математика,
автор: xxxmangoxxx8