Помогите задачи 3,4,5! Решить по заданию. Бредовое решение-жалоба! Норм.решение 35б!!!
Ответы
Ответ:
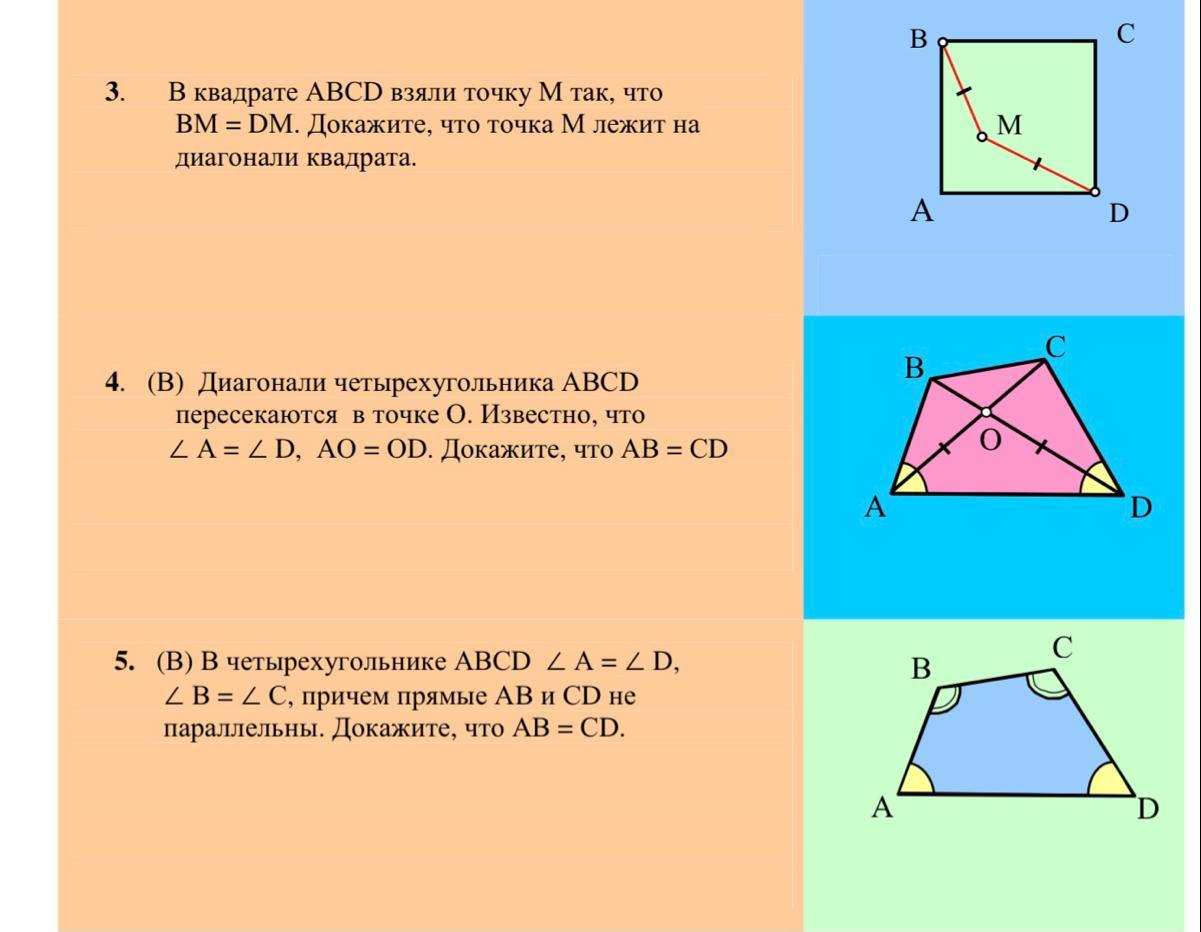
1. В квадрате ABCD точка М пересечения диагоналей АС и ВD совпадает с центром О ,описанной вокруг квадрата окружности. Т.е. в данном случае точка О и точка М - налагаются друг на друга, но, одновременно точка О и точка М принадлежат диагоналям квадрата АС и ВD .Однако ,чтобы точка М лежала на диагонали квадрата не обязательно совпадение точки О и М. Точка М также может принадлежать только одной диагонали ,например АС, и тогда условие ВМ=DМ также выполняется. Таким образом ,условие принадлежности точки М к диагонали квадрата выполняется.
2. АО = OD - по условию
ВО = ОС - по условию
угол ВОА = угол СОD - как вертикальные углы
Значит, тр. ВОА = тр. СОD по двум сторонам и углу между ними.
В равных треугольниках соответственно равные элементы: стороны и углы.
Из этого следует, что АВ = CD , что и требовалось доказать.
3. AB и CD не параллельны, следовательно пересекаются, пусть в точке E.
AED - равнобедренный (углы при основании равны), AE=DE
BEC - равнобедренный (углы EBC и ECB равны как смежные с равными), BE=CE
AE-BE=DE-CE => AB=CD