Question

Здравствуйте, помогите пожалуйста​

Answer 1

Ответ:

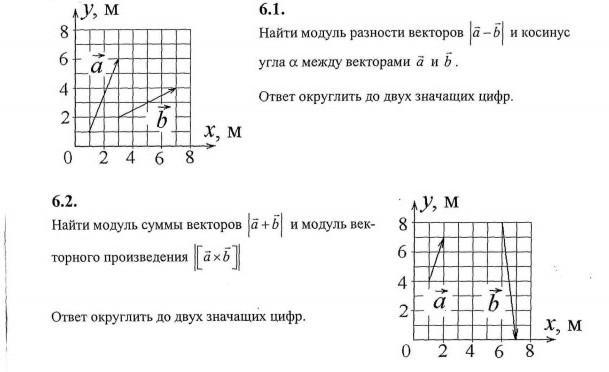
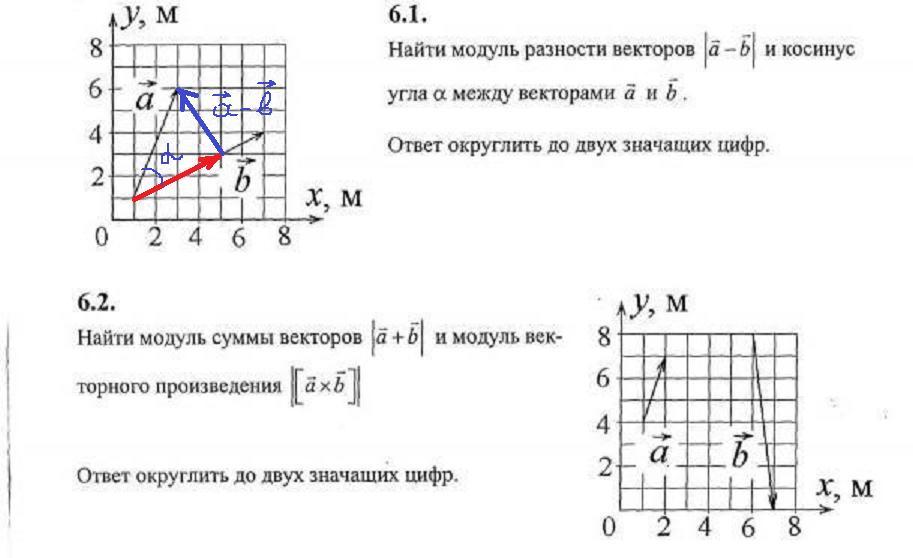
6.1. Разность векторов показана на рисунке. Здесь проще всего воспользоваться тем, что координаты векторов известны, действительно

$\vec{a}(2;5)$ и $\vec{b}(4;2)$

Значит вектор их разности будет иметь координаты, равные разности координат векторов

$\vec{c}=\vec{a}-\vec{b}; \vec{c}(-2;3)$

Значит его модуль

$c=\sqrt{(-2)^2+3^2}=3.6$

Косинус угла между векторами также можно найти по их координатам

$cos\alpha =\frac{2*4+5*2}{\sqrt{2^2+5^2}\sqrt{4^2+2^2} }=0.75$

6.2. Также сначала выпишем координаты векторов

$\vec{a}(1;3); \vec{b}(1;-8)$

Координаты вектора их суммы

$\vec{c}(2;-5)$

Его модуль

$c=\sqrt{2^2+(-5)^2}=5.4$

Векторное произведение найдем как определитель матрицы

$[\vec{a}\times \vec{b}]=\left[\begin{array}{ccc}\vec{i}&\vec{j}&\vec{k}\\1&3&0\\1&-8&0\end{array}\right]=0-8\vec{k}+0-3\vec{k}-0-0=-11\vec{k}$

Модуль его равен просто 11.