Предмет: Геометрия,
автор: Кукарекс
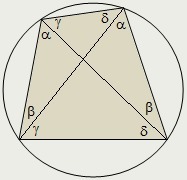
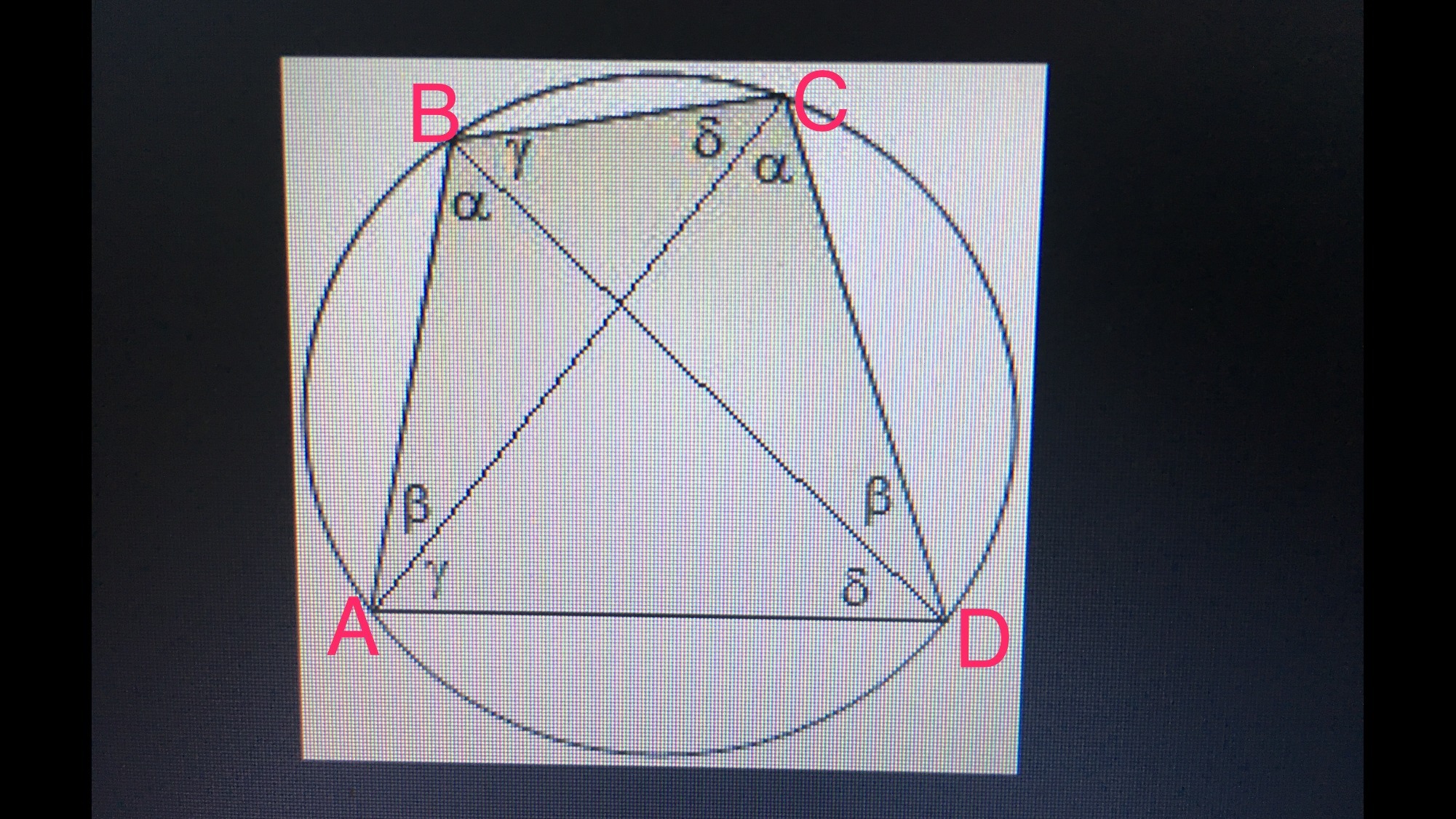
Докажите признак вписанного четырёхугольника. Если угол между стороной и диагональю четырехугольника равен углу между другой диагональю и противоположной стороной то вокруг этого четырёхугольника можно описать окружность
Приложения:
Ответы
Автор ответа:
0
В треугольнике АВД по теореме синусов R=AD/sinα.
Также в тр-ке ACD R=AD/sinα.
1. Для треугольников АВD и ACD радиус описанной окружности одинаков, при этом они имеют общую сторону АД, значит их центры описанных окружностей совпадают, следовательно около четырёхугольника АВСD можно провести окружность.
Доказано.
2. Углы АВД и АСД лежат напротив стороны АД, значит можно сказать, что они вписанные и опираются на общую дугу АД, значит точки А, В, С и Д лежат на одной окружности, следовательно четырёхугольник АВСД - вписанный.
Доказано.
Также в тр-ке ACD R=AD/sinα.
1. Для треугольников АВD и ACD радиус описанной окружности одинаков, при этом они имеют общую сторону АД, значит их центры описанных окружностей совпадают, следовательно около четырёхугольника АВСD можно провести окружность.
Доказано.
2. Углы АВД и АСД лежат напротив стороны АД, значит можно сказать, что они вписанные и опираются на общую дугу АД, значит точки А, В, С и Д лежат на одной окружности, следовательно четырёхугольник АВСД - вписанный.
Доказано.
Приложения:
Автор ответа:
0
Спасибо
Автор ответа:
0
А ту уверен что это обратное свойство работает?
Автор ответа:
0
Ещё раз, логика.
Автор ответа:
0
По-другому не бывает.
Автор ответа:
0
Ясно
Похожие вопросы
Предмет: Математика,
автор: oceanssnaecogmailcom
Предмет: Математика,
автор: yaqub88
Предмет: Информатика,
автор: nastjaskremetova2012
Предмет: Математика,
автор: Нера11
Предмет: Математика,
автор: nigarrzayeva1