Question

Задача на векторы. Ответ отмечен, мне нужно объяснение

Answer 1

Ответ:

$3\sqrt{3}$

Пошаговое объяснение:

По правилу многоугольника, сумма векторов:

$\overrightarrow{OR}+\overrightarrow{RF}+\overrightarrow{FE}=\overrightarrow{OE}$

см. рис. 1

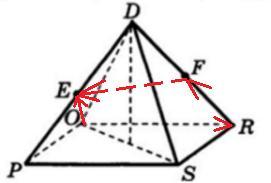
Рассмотрим ΔPDO (см. рис. 2)

Так как все ребра пирамиды равны, значит ΔPDO - равносторонний.

Е-середина PD, следовательно ОЕ - медиана ⇒ DE=PE=PD/2=6/2=3

Но так как ΔPDO - равносторонний, то ОЕ также и высота

Из прямоугольного треугольника DEO находим катет ОE:

$OE=\sqrt{DO^2-DE^2} =\sqrt{6^2-3^2}= \sqrt{27}=\sqrt{9*3} =3\sqrt{3}$

Answer 2

Ответ:

По правилу треугольника сложения векторов имеем:

$\overline{OR}+\overline{RF}=\overline{OF}\\\\\overline{OF}+\overline{FE}=\overline{OE}\ \ \Rightarrow \\\\\overline{OR}+\overline{}RF+\overline{FE}=\overline{OE}$

Так как треугольник POD - равносторонний и точка Е - середина PD , то ОЕ - высота (медиана и биссектриса) равностороннего треугольника.

$OE=\sqrt{OP^2-PE^2}=\sqrt{6^2-3^2}=\sqrt{36-9}=\sqrt{27}=\sqrt{9\cdot 3}=3\sqrt3$

$|\overline{OE}|=3\sqrt3$