Question

ПОМОГИТЕ ПОЖАЛУЙСТА с задачкой​

Answer 1

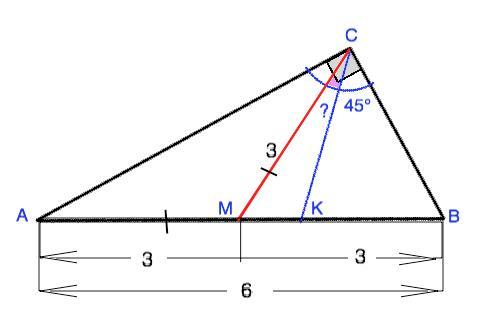
  Вычислите угол между биссееткрисой и медианой, проведенными из прямого угла прямоугольного треугольника площадью (9√3)|2 и гипотенузой 6.

——————

Объяснение (подробно)

   Пусть в ⊿ АВС угол С=90°, СМ- медиана, СК - биссектриса.

Биссектриса треугольника делит угол, в котором проведена,  пополам. => угол АСК=ВСК=45°

  Медиана прямоугольного треугольника, проведенная к гипотенузе, равна её половине => СМ=АМ=ВМ=6:2=3.

 Медиана треугольника делит его на два равновеликих.

S(ACM)=S(BCM)=0,5•(9√3)/2=(4,5√3)/2

  По одной из формул площадь треугольника равна половине произведения сторон на синус угла между ними. =>

S (AMC)=AM•MC•sin(AMC):2=>

sin(AMC)= 2•S(AMC):AM•MC

sin(AMC)= (9√3)/2):9=(√3)/2 - это синус 120°, т.к. угол АМС - тупой.

 В равнобедренном треугольнике АМС острые углы равны.  

∠АСМ=∠САМ=(180°-120°):2=30°=>

∠КСМ=∠АСК-∠АСМ=45°-30°=15°– это ответ.