Question

ПОМОГИТЕ ПОЖАЛУЙСТА с задачкой​

Answer 1

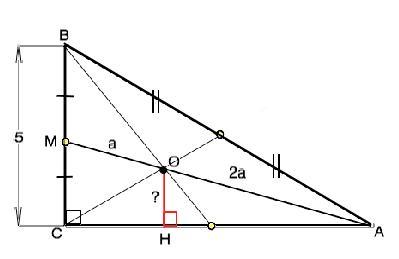
  Один из катетов прямоугольного треугольника равен 5. Найдите расстояние от точки пересечения медиан до второго катета.

—————

Ответ: D) 1²/₃ (ед. длины)

  Расстоянием от точки до прямой считается длина отрезка,  который соединяет  эту точку с данной прямой и перпендикулярен ей.

  Пусть в треугольнике АВС угол С=90°, катет ВС=5, точка О - пересечение медиан, М - середина ВС, ОН - искомое расстояние.

Медианы треугольника пересекаются в отношении 2:1, считая от вершины. ⇒

В ∆ САМ точка О делит АМ в отношении АО:ОМ=2:1 ⇒

АМ=АО+ОН=3 части.

Прямоугольные треугольники САМ и НАО подобны по общему острому углу.

Поэтому СМ:НО=АМ:АО=3:2

СМ=ВС/2=2,5

ОН=2,5•2:3=1 ²/₃ (ед. длины)