Предмет: Математика,
автор: Аноним
Ещё один интеграл! Прощу помощи зала! Очень нужно.
Приложения:
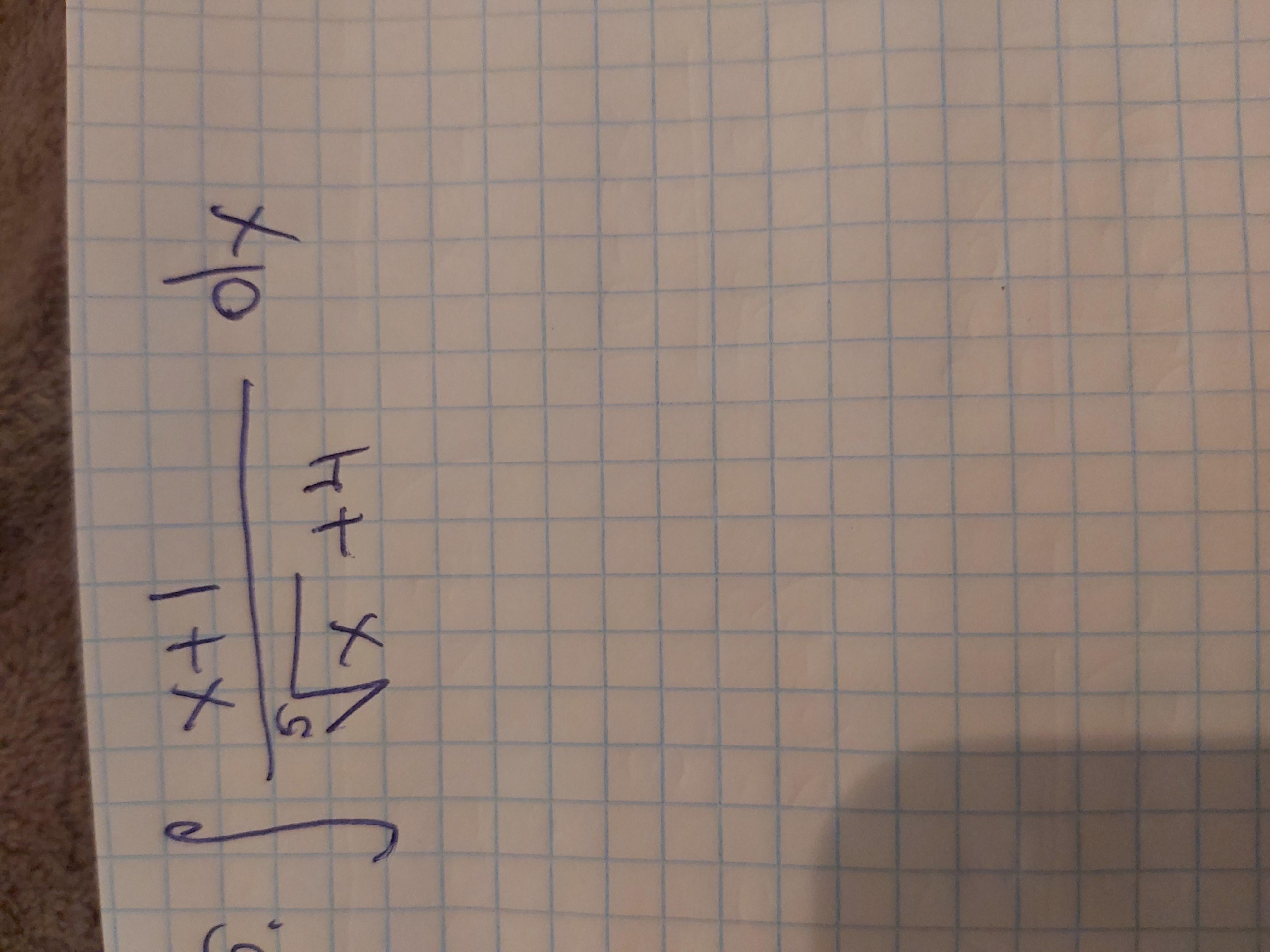
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Сделаем замену переменной:
Разделим в подынтегральном выражении многочлен в числителе на многочлен в знаменателе, это можно сделать либо "в столбик", либо по схеме Горнера, компактнее будет по второму варианту:
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0
-4| 1 | -4| 16|-64|256|-1023|4092|-16368|65472|-261888
То есть после деления имеем:
Возвращаясь к исходной замене, получаем:
6575:
Видимо, поиздеваться. Если б 4 в знаменателе заменили на 1 решение было бы гораздо быстрее и более симпатичное ¯\_(ツ)_/¯
Похожие вопросы
Предмет: Русский язык,
автор: okunaika26
Предмет: Русский язык,
автор: ЧебурашкаХD
Предмет: Английский язык,
автор: Zakaryan1999
Предмет: Информатика,
автор: arseniydmitrie
Предмет: Биология,
автор: zay9