Предмет: Алгебра,
автор: nikitos1974
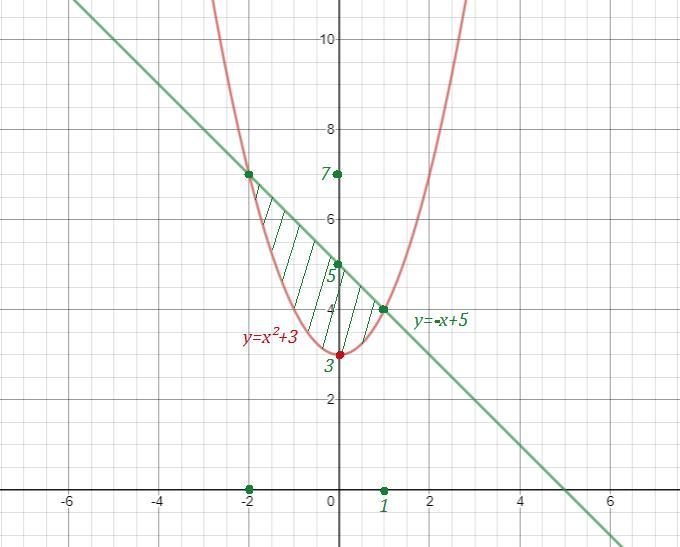
Найти площадь фигуры ограниченной линии y=x^2+3, y=-x+5 Если можно с рисунком
Ответы
Автор ответа:
0
Ответ:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sas4481
Предмет: Українська мова,
автор: Alionella
Предмет: Русский язык,
автор: король2002
Предмет: Алгебра,
автор: Hkolaaaa