Предмет: Математика,
автор: tatyanaperova00
помогите, пожалуйста, решить предел)))
Приложения:
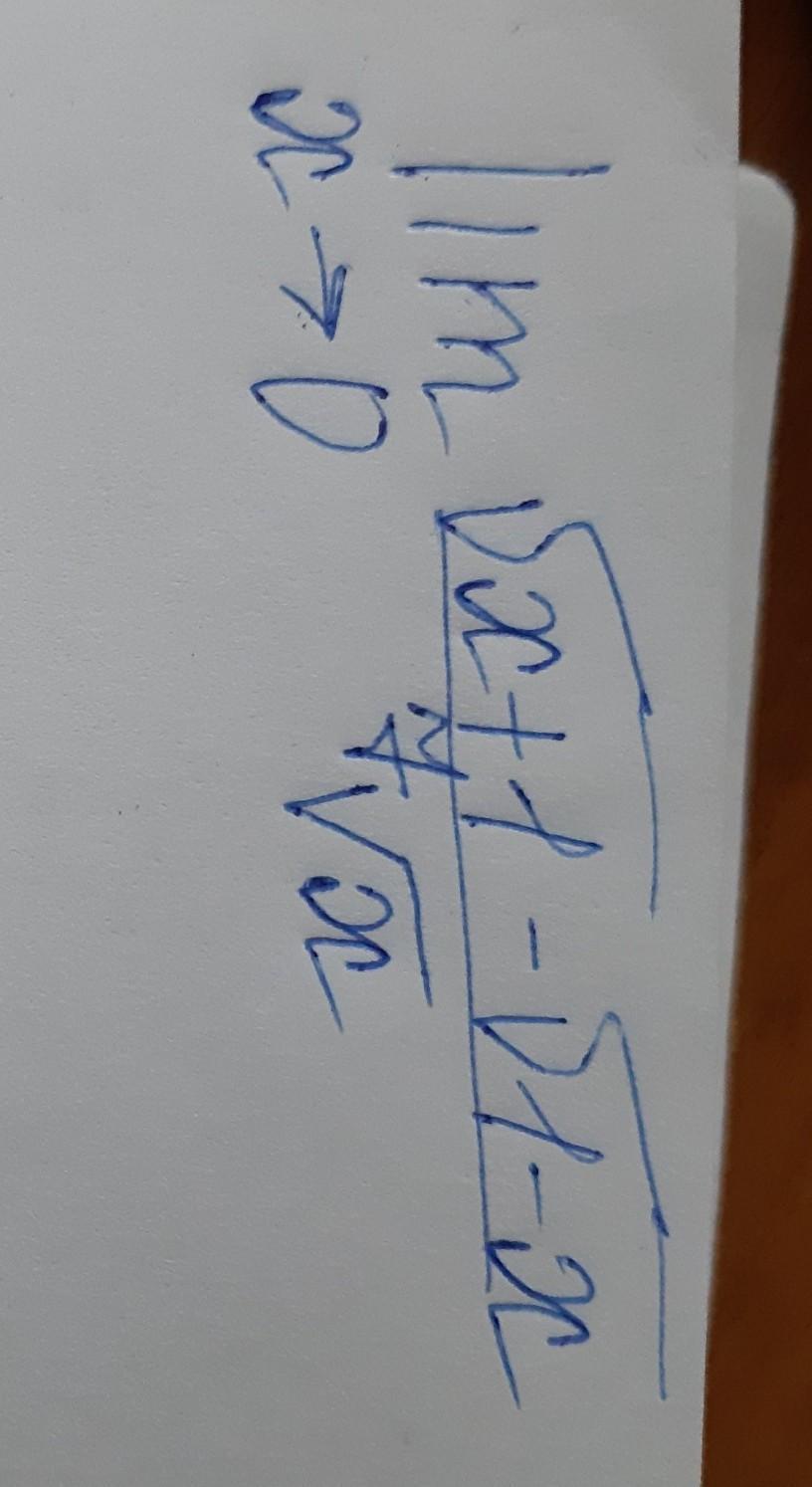
Ответы
Автор ответа:
1
Ответ:
0
Пошаговое объяснение:
В окрестности нуля штуку сверху можно разложить в ряд и получить, что
и
(о малые (или большие) писать не стал)
Подставив в предел получим что-то вроде
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Геометрия,
автор: mi3177441
Предмет: Математика,
автор: ishenkosofia1011
Предмет: Алгебра,
автор: alchikks
Предмет: Химия,
автор: жироввадим