Предмет: Математика,
автор: 40538385959
Обчислити об'єми тіл, утворених обертанням навколо осі OY фігур, обмежених зазначеними лініями:
Приложения:
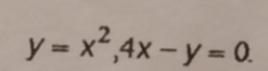
Ответы
Автор ответа:
3
Ответ:
Объем тела, образованного вращением вокруг оси OY равен ед.³
Пошаговое объяснение:
Вычислить объем тела, образованного вращением вокруг оси OY фигур, ограниченных указанными линиями:
y = x²; 4x - y = 0
Формула для нахождения объема тела вращения вокруг оси Оу:
У нас
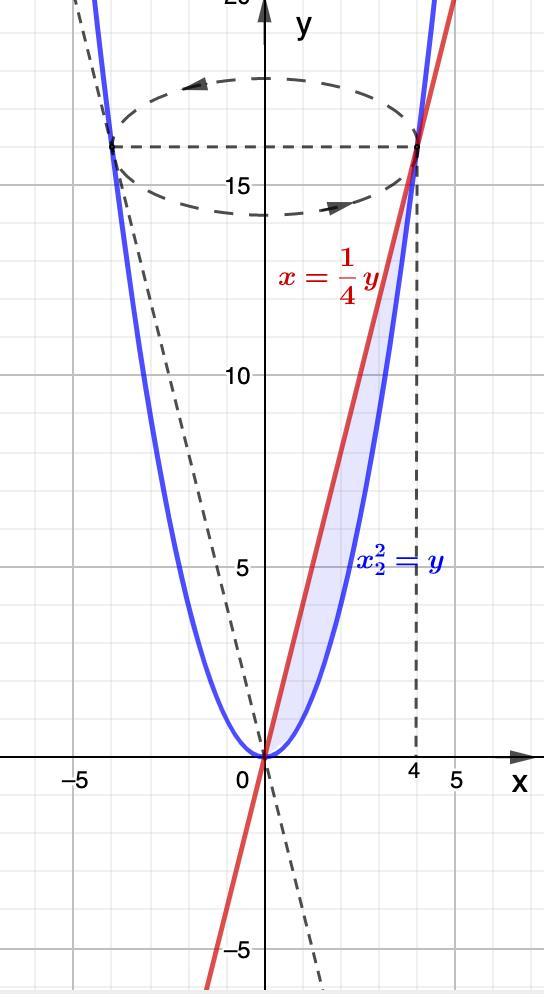
Найдем пределы интегрирования из равенства:
Вычислим объем:
Объем тела, образованного вращением вокруг оси OY равен ед.³
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: fevralek2006
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: Yana1111116
Предмет: Русский язык,
автор: service4
Предмет: Українська мова,
автор: winst51