Предмет: Алгебра,
автор: shemchik
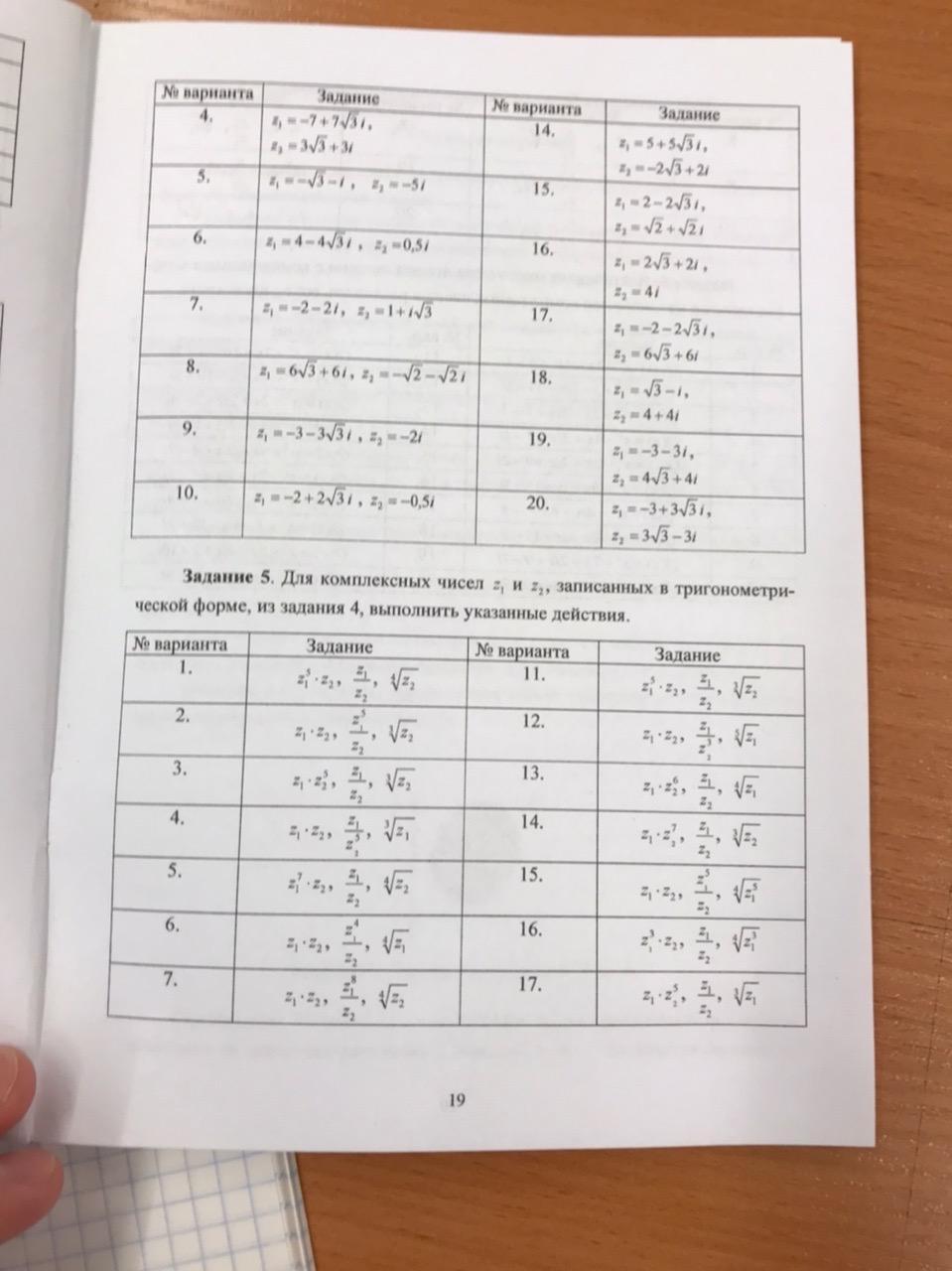
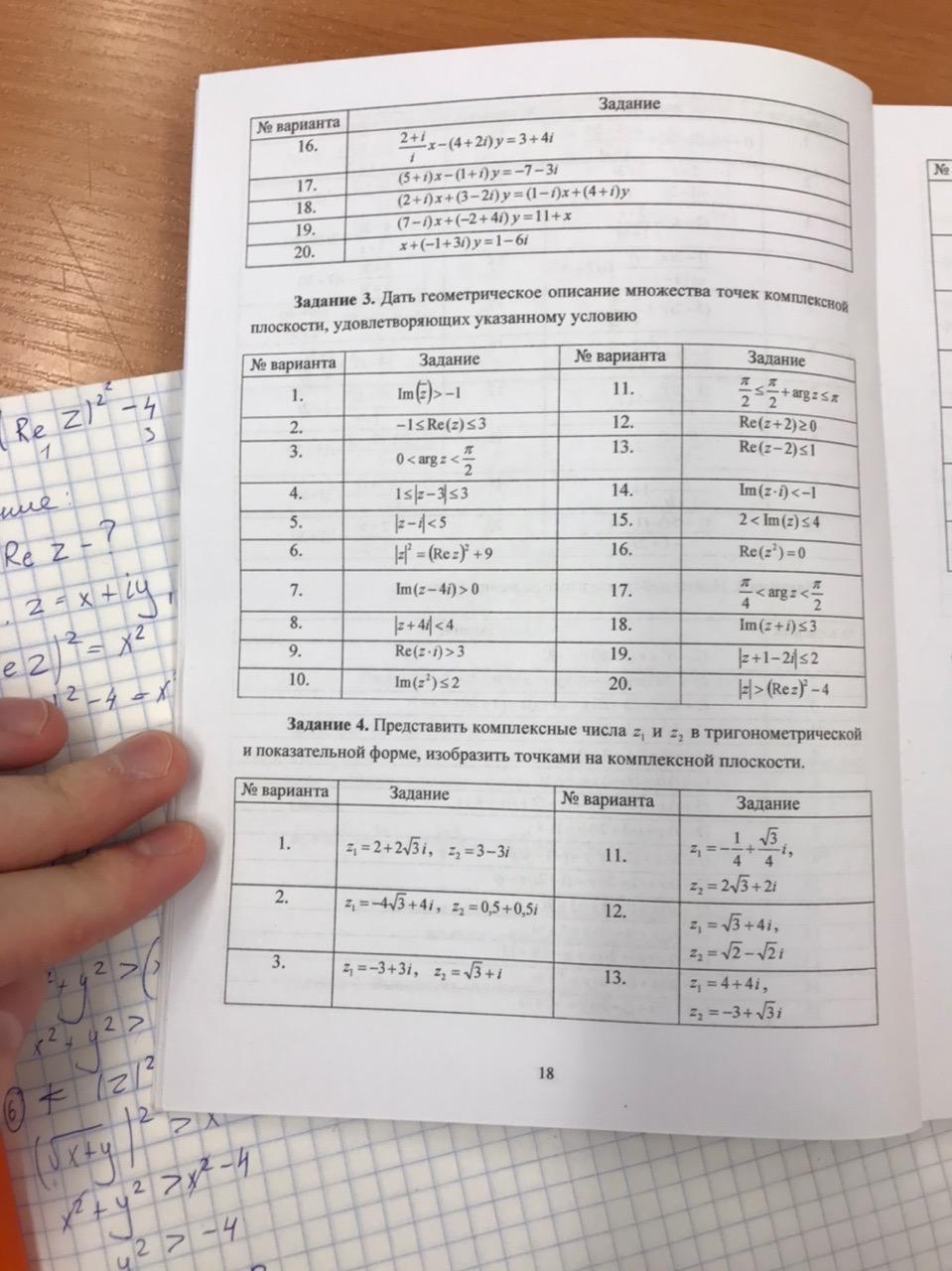
Помогите пожалуйста решить. Номер 4, 7 вариант.
Приложения:
Ответы
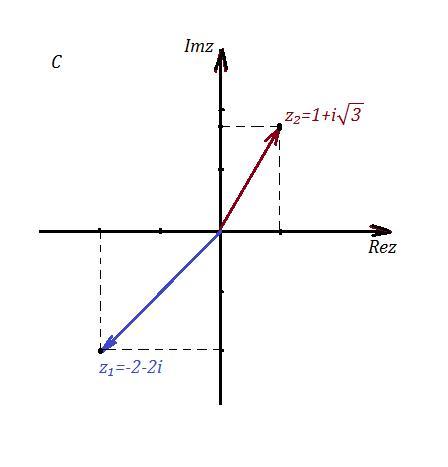
Автор ответа:
0
Приложения:
Похожие вопросы
Предмет: Математика,
автор: albina1980ab
Предмет: Математика,
автор: igortrof2010
Предмет: Математика,
автор: Popovichinna1970110
Предмет: Математика,
автор: ррил
Предмет: Математика,
автор: Аноним