Предмет: Геометрия,
автор: Cypookk
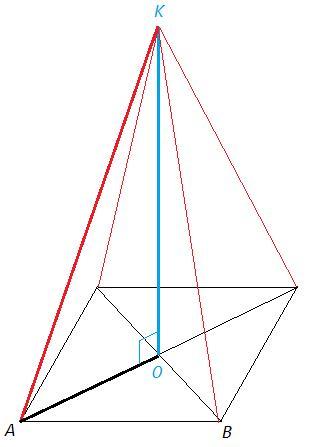
Через центр пересечения диагоналей квадрата АВСД проведена перпендикуляр ОК к плоскости этого квадрата. Найти расстояние от точки К до вершин квадрата, если сторона квадрата равна 8см, а ОК=10см
Ответы
Автор ответа:
0
Диагонали квадрата перпендикулярны, равны, точкой пересечения делятся пополам.
Сторона квадрата 8, половина диагонали AO=4√2 см.
Перпендикуляр к плоскости перпендикулярен любой прямой в плоскости.
AOK=90, из треугольника AOK по теореме Пифагора
AK= √(AO^2+OK^2) =√(32+100) =√132 =2√33 (см)
Треугольники AOK и BOK равны по двум катетам, AK=BK. Аналогично с остальными вершинами, точка K равноудалена от вершин основания.
(Пересечение диагоналей прямоугольника - центр описанной окружности. Если вершина пирамиды проецируется в центр описанной окружности основания - боковые ребра равны.)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Dsrtcvjb
Предмет: Математика,
автор: yunboomboomboom
Предмет: Физика,
автор: shultsannashults
Предмет: Литература,
автор: Anqelalove