Предмет: Геометрия,
автор: abrosimovan426
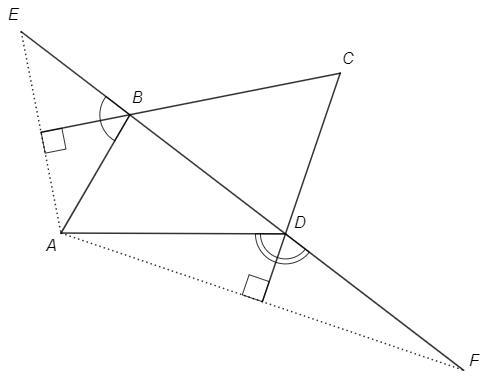
ABCD выпуклый четырехугольник, в котором угол BAD=60, а точки E и F симметричны точке А относительно прямых CB и CD соответственно. Известно также, что точки B, D, E, F лежат на одной прямой. Докажите, что угол BCD=60. С рисунком, пожалуйста.
siestarjoki:
BCD - угол между биссектрисами внешних углов треугольника BAD. BCD= 90 -BAD/2
Ответы
Автор ответа:
3
Точки A и E симметричны относительно прямой BC - значит BC является серединным перпендикуляром к AE. По свойству равнобедренного треугольника BC является биссектрисой ABE, то есть биссектрисой внешнего угла треугольника BAD. Аналогично DC. BCD - угол между биссектрисами внешних углов треугольника BAD.
BCD= 90 -BAD/2 =90 -60/2 =60
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: ekaterinarogalina5
Предмет: Экономика,
автор: korobkov470valentun
Предмет: Информатика,
автор: Python444
Предмет: Математика,
автор: svetaaa77