Предмет: Геометрия,
автор: kaneki13449047
Большая диагональ ромба 18 см, а тупой угол 120°. Найдите площадь ромба.
Должно получиться 54√3 см в квадрате.
Ответы
Автор ответа:
10
Ответ:
1.АО=1/2 АС(по св-ву параллелограмма)
2. Т.к. АВСD- ромб, то угол ВОА=90°, угол АВО=60°, а угол ВАО=30°
3. тр. АВО- прямоугольный, по т.Пифагора АВ^2=ВО^2+АО^2.
По свойству угла в 30°, в прямоугольном треугольнике напротив угла в 30° лежит катет, который равен половине гипотенузы, т.е. АВ=2ВО
Пусть ВО=х, АВ=2х, тогда 4х^2=х^2+81
3х^2=81
х^2=27
х=3√3- ВО
Sтр.АВС=ВО×АС×1/2=3√3×18=54√3/2=27√3
S ABCD= 2 S ABC= 54√3
Приложения:
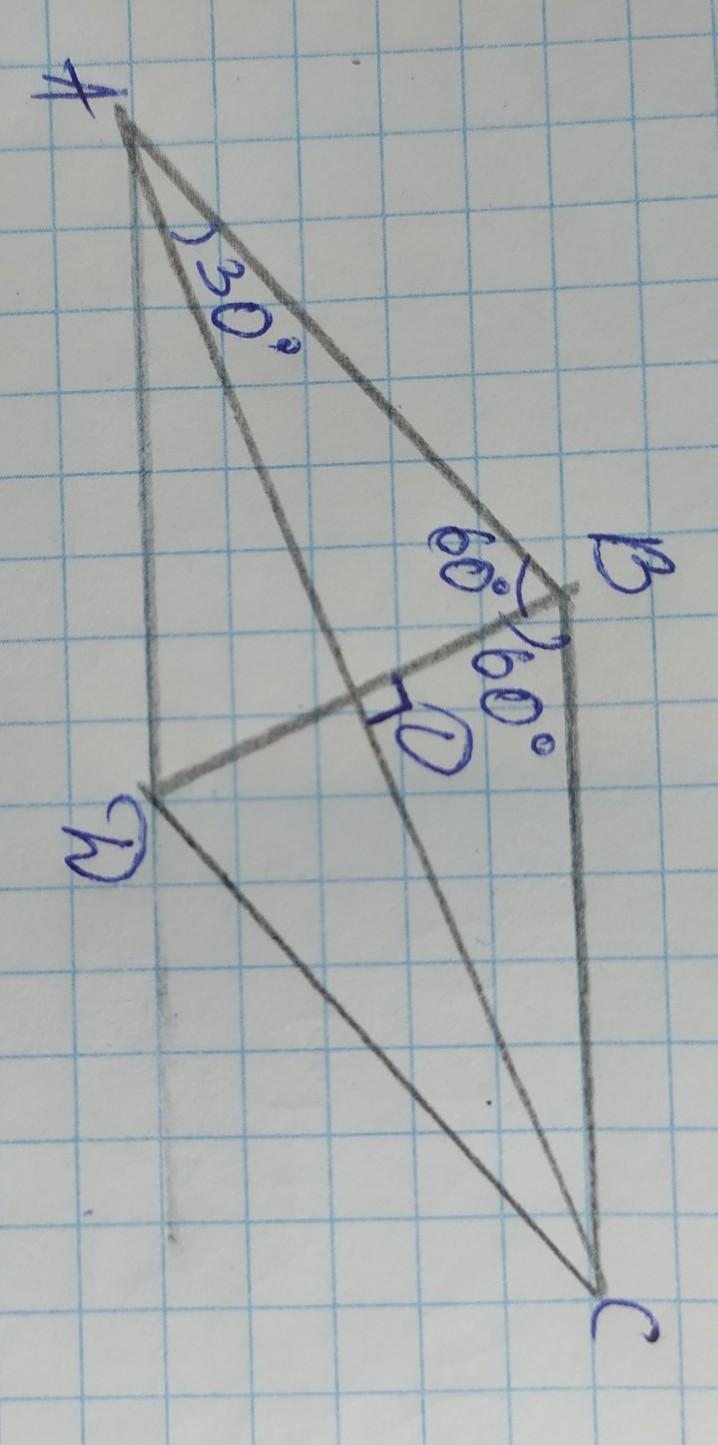
Похожие вопросы
Предмет: Математика,
автор: vosstanovitdoynik777
Предмет: Алгебра,
автор: 777kot777alex
Предмет: Алгебра,
автор: 777kot777alex
Предмет: История,
автор: asya0812
Предмет: Математика,
автор: saida86