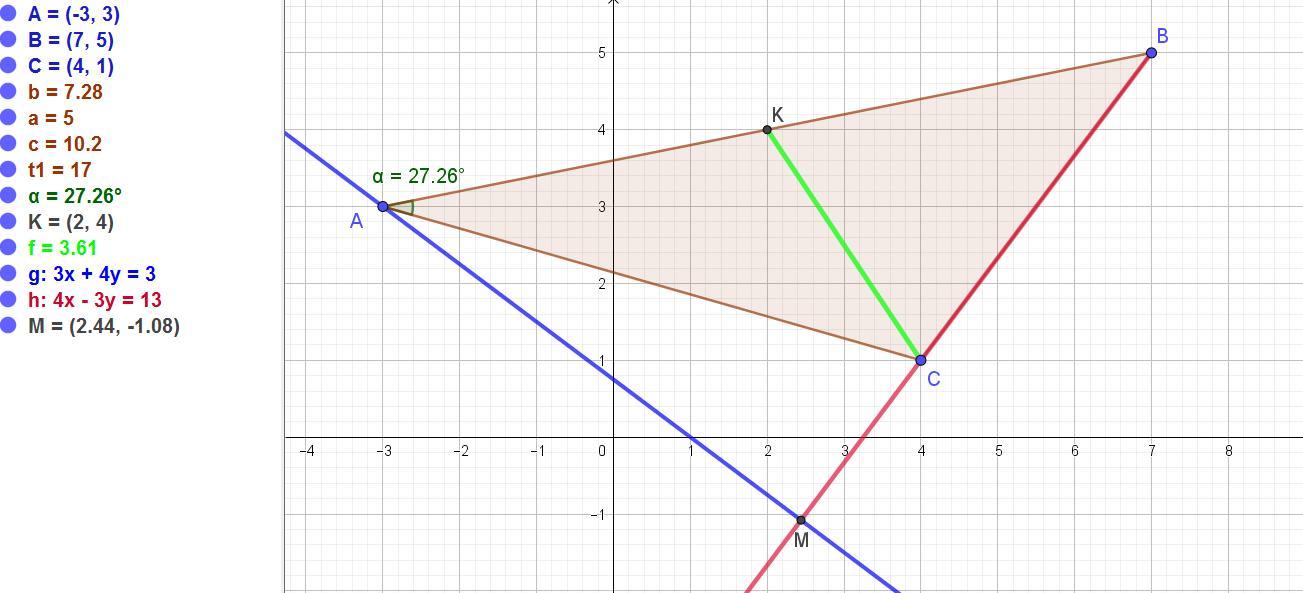
Даны координаты вершин треугольника А, В, С. Найти уравнения сторон АВ и АС, угол между ними, уравнения медианы СК и высоты АМ. Сделать чертеж треугольника.
А B C
(-3, 3) (7, 5) (4, 1)
Ответы
Даны координаты вершин треугольника А (-3, 3), В (7, 5), С (4, 1).
1) Уравнение прямой AB.
Вектор АВ = ((7-(-3)=10; 5-3=2) = (10; 2).
Каноническое уравнение прямой: (x + 3)/10 = (y - 3)/2.
2х - 10у + 36 = 0, или, сократив на 2:
х - 5у + 18 = 0 это общее уравнение.
у = (1/5)х + (18/5) это уравнение с угловым коэффициентом.
2) Уравнение прямой AС.
Вектор АС = ((4-(-3)7; 1-3=-2) = (7; -2).
Каноническое уравнение прямой: (x + 3)/7 = (y - 3)/(-2) .
2х + 7y - 15 = 0 это общее уравнение.
у = (-2/7)х + (15/7) это уравнение с угловым коэффициентом.
3) Найти угол между векторами АВ = {10;2} и АС = {7; -2}.
Решение: Найдем скалярное произведение векторов:
a·b = 10 · 7 + 2 · (-2) = 70 - 4 = 66.
Найдем модули векторов:
|a| = √(10² + 2²) = √(100 + 4) = √104 ≈ 10,198.
|b| = √(7² + (-2)²) = √(49 + 4) = √53 ≈ 7,28.
Найдем угол между векторами:
cos α = a · b = 66 = 0,888975.
|a| · |b| √104*√53
Угол А равен arc cos0,888975 = 0,4757 радиан или 27,255 градусов .
4) Находим координаты точки К как середину отрезка АВ.
К((-3+7)/2=2; (3+5)/2=4) = (2; 4). Вектор СК: (-2; 3).
Уравнение медианы СК: (х - 4)/(-2) = (у -1)/3.
3х + 2у - 14 = 0.
у = (-3/2)х + 7.
Угловой коэффициент прямой ВС равен к(ВС) = (1-5)/(4-7) = 4/3.
Тогда угловой коэффициент перпендикуляра к ВС равен:
к(АМ) = -1/(к(ВС) = -1/(4/3) = (-3/4).
Уравнение АМ: у = (-3/4)х + в.
Для определения параметра в подставим координаты точки А:
3 = (-3/4)*(-3) + в. Отсюда в = 3 - (9/4) = 3/4.
Уравнение высоты АМ: у = (-3/4)х + (3/4).