Предмет: Математика,
автор: Allena2000
помогите пожалуйста
Приложения:
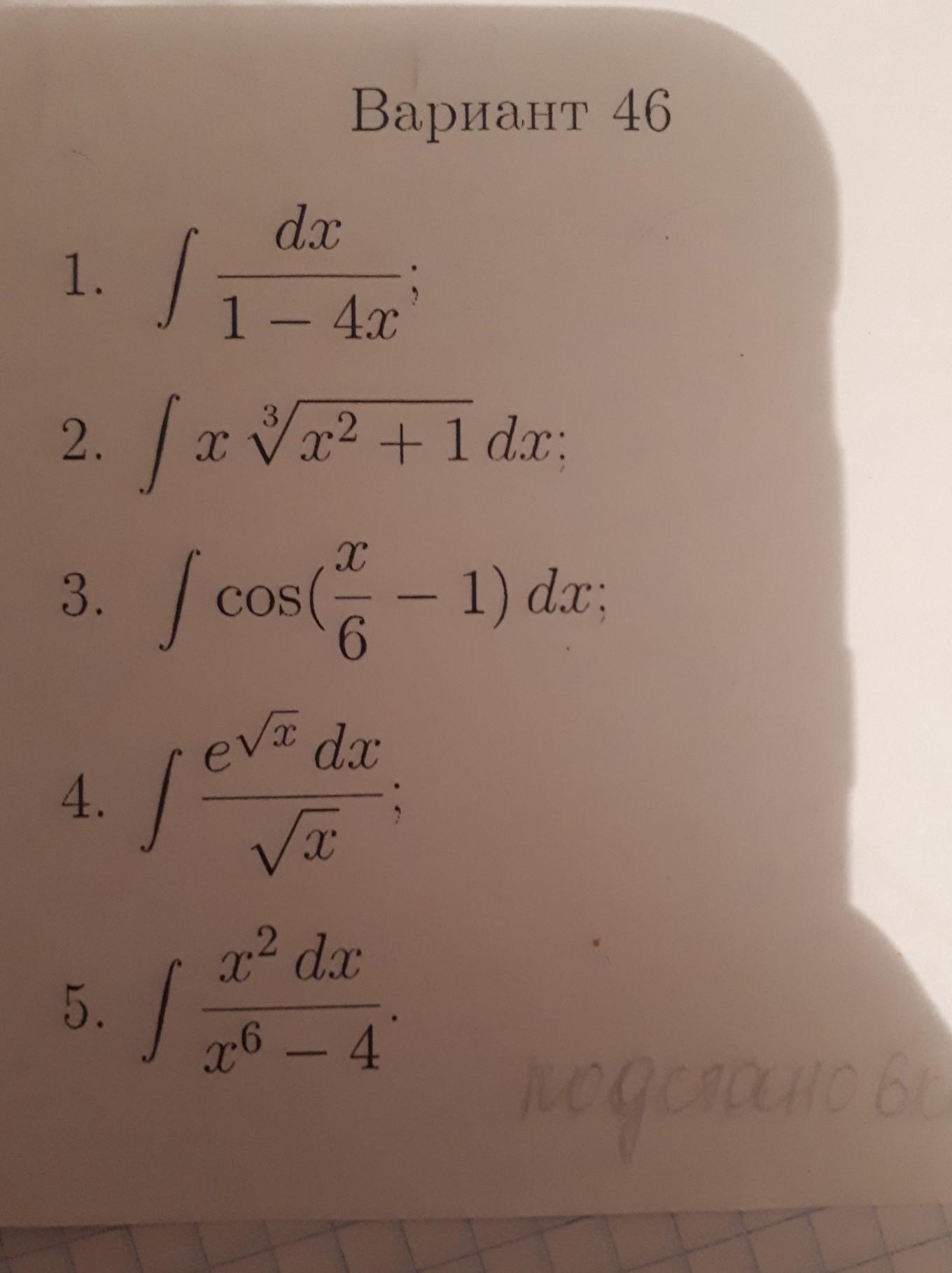
Ответы
Автор ответа:
1
1.
u=1-4x
du=(1-4x)`dx
du=-4dx
d(1-4x)=-4dx
2.
Аналогично
u=x²+1
du=2xdx
d(x^2+1)=2xdx
3
u=(x/6)-1
du=dx/6
4.
u=√x
du=dx/(2√x)
5.
u=x³
du=3x²dx
Похожие вопросы
Предмет: Биология,
автор: aoaoooa
Предмет: Алгебра,
автор: KoloFern
Предмет: Алгебра,
автор: lerashkvyria
Предмет: География,
автор: дмитрий342
Предмет: Математика,
автор: dmitryabramov