Предмет: Геометрия,
автор: xoinveins
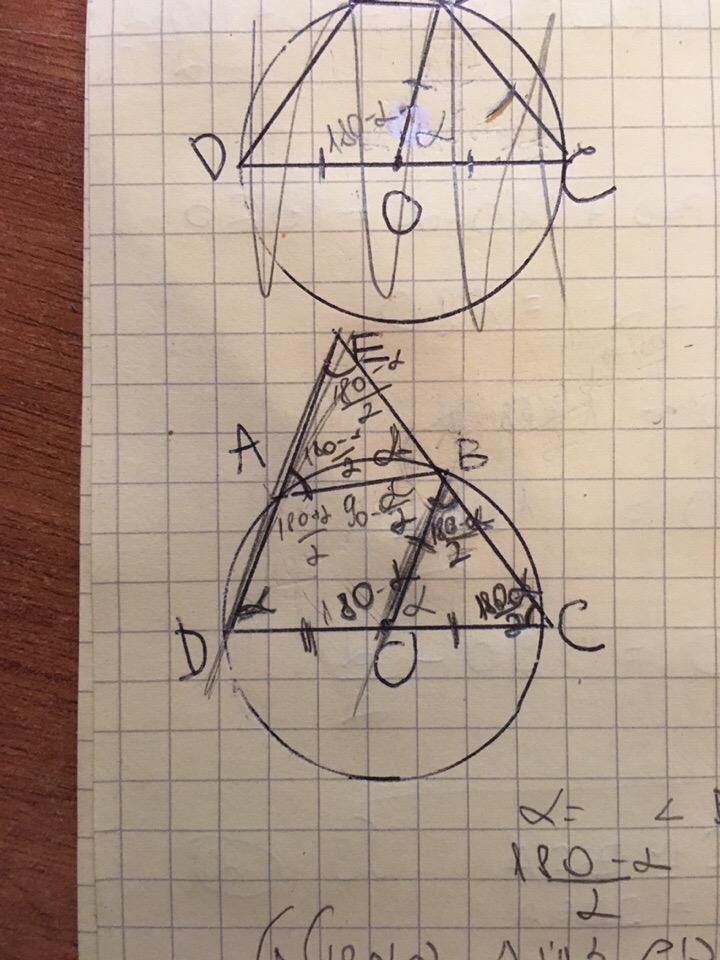
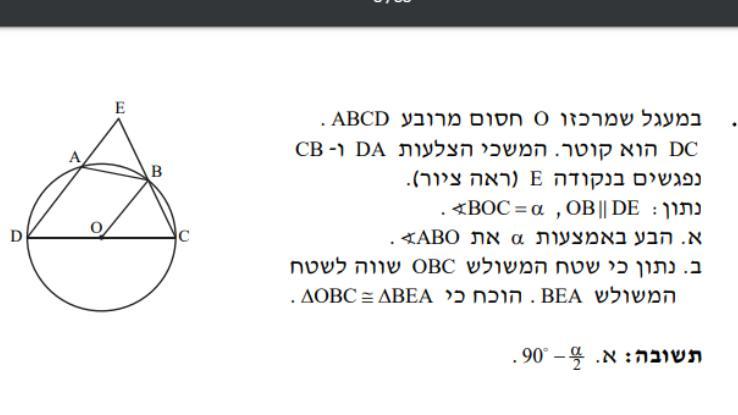
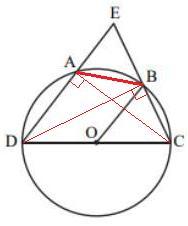
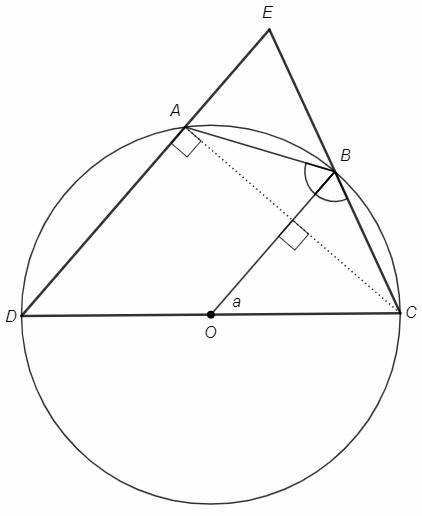
в окружности центр которой точка O вписан четырехугольник ABCD. DC это диаметр. продолжения сторон DA и CB встречаются в точке E. OB параллельно DE, угол BOC=α. дано: площадь треугольника OBC равна площади треугольника BEA.нужно доказать что треугольник OBC≅BEA.
Приложения:
Аноним:
А что в условии написано про угол ABO?
в первой части задания надо было выразить его через α как 90-α/2... я с этим заданием несколько часов уже сижу... судя по тому, что упоминается, что площади этих 2 треугольников равны, это должно как-то использоваться в доказательстве равенства. obc и aeb не могут быть равносторонними, потому что углы там разные, если выразить их через α. и я понятия не имею как в таком случае можно использовать равенство площадей
Вижу в условии на картинке про угол АВО есть, а эту часть вы не перевели на русском
это уже не условие, а первая часть задания, где надо было выразить ABO через α (90-α/2), я подумала, что для доказательства равенства это не особо играет роли... извиняюсь, если ошиблась
Возможно кто-то решит заранее.. Сейчас я откланяюсь .
в любом случае, спасибо вам большое!
да они не просто подобны, а равны. Я вроде решил.. Решение в 2 строчки..
ошибся, в 3 строчки ... :)
у, в какие дебри все полезли... а ларчик просто открывался.
мне уже места нет, чтоб выложить решение... кстати, что означает знак ≅ в условии ( простите любителя за такой вопрос)
Ответы
Автор ответа:
0
∠DAC=∠DBC=90 (вписанные углы, опирающиеся на диаметр)
△DEB~△CEA (прямоугольные с общим углом E)
DE/CE=EB/EA
△BEA~△DEC (по двум пропорциональным сторонам и углу между ними)
△OBC~△DEC (по двум соответственным углам при OB||DE)
△BEA~△OBC
-------------------------------------------------------------
Найдем угол ABO.
DA⊥AC, OB||DA => OB⊥AC
Радиус OB перпендикулярен хорде AC, следовательно является биссектрисой угла ABC, ∠ABO=∠CBO
Треугольник BOC - равнобедренный (OB=OC, радиусы)
∠CBO= (180-a)/2 =∠ABO
Приложения:
добавляете что и где? нич-ч-ч-его не вижу. :) кстати, что означает знак ≅ в условии ( простите любителя за такой вопрос)
А... Понял. Я не использовал то, что площадь OBC равна площади BEA. Только сейчас заметил.
во! вот это и главное. а угол альфа для отвлекухи дан
Угол дан чтобы найти угол ABO.
А доказывать надо было конгруэнтность (равенство), а не подобие. Я был совсем невнимателен с этой задачей.
равенство доказывается без угла альфа. могу дать решение но не знаю куда...
https://znanija.com/task/32620691
ща, оформить хоть как-то надо :)
Мне всё-таки непонятно. Почему на иврите дан ответ 90 -a/2. Это ответ без учета равенства площадей. При равных площадях ответ 60.
да потому что там задают задачи такие же задавальщики, как и у нас, не думая.
Похожие вопросы
Предмет: Алгебра,
автор: hdhdhdhddhhdhd
Предмет: Українська мова,
автор: voenuymun
Предмет: Математика,
автор: maria2009jmv
Предмет: Алгебра,
автор: ььтттиао
Предмет: География,
автор: дмитрий342