29 гномов пошли в лес за грибами. Когда они вернулись, оказалось, что подосиновики были в 1616 корзинах, подберезовики в 1717, белые – в 1111. При этом в 77 корзинах были и подосиновики, и подберезовики, в 66 – подосиновики и белые, в 55 – подберезовики и белые, а в одной корзине были все три вида грибов. И только у некоторых гномов были одни сыроежки. Сколько гномов принесли одни сыроежки?
Ответы
Ответ:
2
Правильное условие:
29 гномов пошли в лес за грибами. Когда они вернулись, оказалось, что подосиновики были в 16 корзинах, подберезовики в 17, белые – в 11. При этом в 7 корзинах были и подосиновики, и подберезовики, в 6 – подосиновики и белые, в 5 – подберезовики и белые, а в одной корзине были все три вида грибов. И только у некоторых гномов были одни сыроежки. Сколько гномов принесли одни сыроежки?
Пошаговое объяснение:
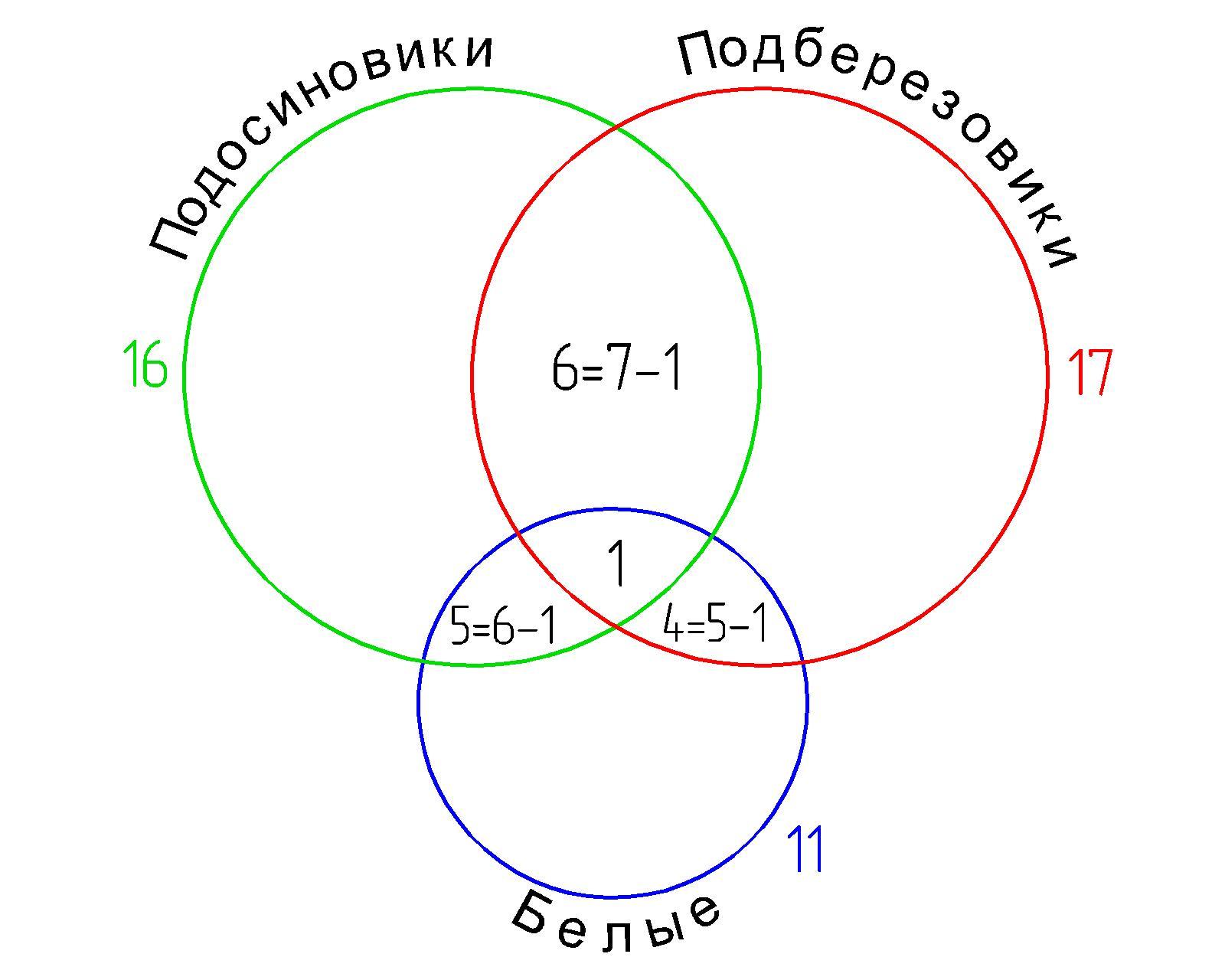
Задача решается с помощью кругов Эйлера.
Построим схему.
1) В 7 корзинах были и подосиновики, и подберезовики, при этом в 1 из них были еще и белые грибы. Значит одновременно подосиновиков и подберезовиков было в 7-1=6 корзинах.
Аналогично,
одновременно подосиновиков и белых было в 6-1=5 корзинах,
одновременно подберезовиков и белых было в 5-1=4 корзинах.
2) Подосиновики встречаются в 16 корзинах, при этом они смешаны с белыми в 5 корзинах, с подберезовиками - в 6 корзинах, и с двумя видами - в 1 корзине. Значит корзин с одними подосиновиками было:
16-6-5-1=4.
Аналогично,
корзин с одними подберезовиками было: 17-6-4-1=6;
корзин с одними белыми грибами было: 11-5-4-1=1.
Тогда корзин с известным содержимым было:
(4+6+1)=11 - по одному виду
(6+5+4+1)=16 - смешанных
Всего корзин с известным содержимым было: 11+16=27.
Значит корзин с сыроежками было: 29-27=2