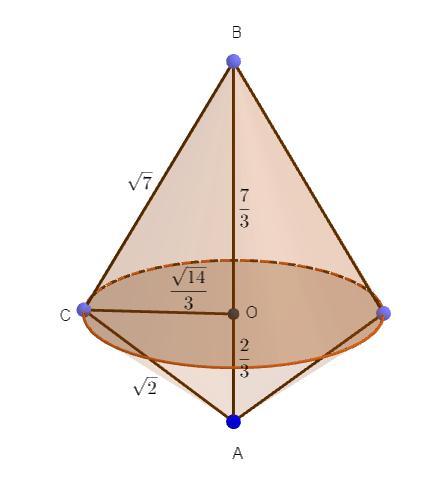
Прямоугольный треугольник с катетами корень из 2 и корень из 7 см вращается вокруг гипотенузы. Найдите объём полученого тела вращения.
Ответы
При вращении прямоугольного треугольника вокруг гипотенузы получается тело вращения, состоящее из двух конусов: конуса с образующей CB (катет Δ ABC) и конуса с образующей CА (катет Δ ABC). Оба конуса имеют равное основание – окружность радиуса CO. Радиус окружности основания конусов – высота CO, опущенная из вершины C ΔABC на гипотенузу AB. Обозначим CO = R.
Объем тела вращения (V) будет равен сумме объемов большого (V₁) и малого (V₂) конусов. V = V₁ + V₂ ;
Объем конуса V = 1/3SoH; So – площадь основания, H – высота конуса.
По т.Пифагора найдем гипотенузу Δ ABC:
AB² = CB² + CA² = 7+2 = 9; AB = 3 см.
Найдем высоту CO Δ ABC. ΔBCO подобен ΔABC по двум углам: <COB = <ACB = 90⁰, <CBA общий. Из подобия треугольников следует:
СO/CB = CA/AB; CO=CA*CB/AB = √2*√7/3 = √14/3 см. Радиус окружности R = √14/3 см.
По т.Пифагора найдем катет BO Δ OBC:
BO² = CB² - CO² = 7-14/9 = (63-14)/9 = 49/9; BO = 7/3 см.
AO = AB – BO = 3 – 7/3 = 2/3.
Sо = πR² = 14π/9 см².
V = V₁ + V₂ = 1/3 * 14π/9*7/3 + 1/3 * 14π/9*2/3 = 1/3*14π/9*(7/3+2/3) = 1/3*14π/9*3 = 14π/9;
Или:
V₁ = 1/3 * 14π/9*7/3 = 98π/81;
V₂ = 1/3 * 14π/9*2/3 = 28π/81;
Объем тела вращения V = V₁ + V₂ = 98π/81+28π/81= 126π/81 = 14π/9 см³.
Объем тела вращения V = 14π/9 см³.