Предмет: Алгебра,
автор: kirilllisus
Найти производную функции
Приложения:
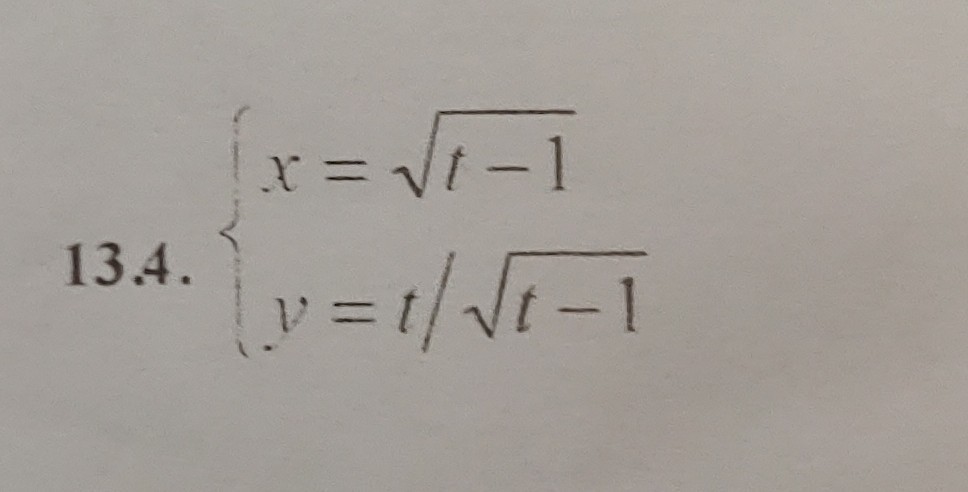
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: Katarina12345678
Предмет: География,
автор: DeRNoV453
Предмет: Биология,
автор: gasnikovilia10
Предмет: Информатика,
автор: Яна1111111777
Предмет: Математика,
автор: ira237