Предмет: Геометрия,
автор: kimruslan
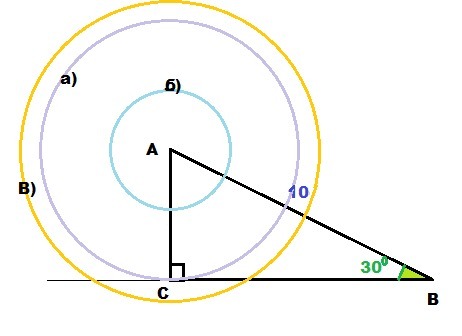
В прямоугольном треугольнике АСВ (∠C = 90°) АВ = 10, ∠ABC = 30°. С центром в точке
А проведена окружность. Каким должен быть ее радиус, чтобы:
а) окружность касалась прямой ВС;
b) окружность не имела общих точек с прямой ВС;
c) окружность имела две общие точки с прямой ВС?
Ответы
Автор ответа:
207
ΔABC - прямоугольный; ∠C = 90°; ∠B = 30°; AB = 10
Катет AC лежит против угла 30° ⇒ равен половине гипотенузы AB:
AC = AB/2 = 10 /2 = 5
Проведена окружность с центром в точке А
а) радиус в точку касания образует с касательной угол 90°.
Радиус равен АС = 5
б) радиус меньше 5
в) радиус больше 5
Катет AC лежит против угла 30° ⇒ равен половине гипотенузы AB:
AC = AB/2 = 10 /2 = 5
Проведена окружность с центром в точке А
а) радиус в точку касания образует с касательной угол 90°.
Радиус равен АС = 5
б) радиус меньше 5
в) радиус больше 5
Приложения:
Похожие вопросы
Предмет: Биология,
автор: vladochka11111125
Предмет: Геометрия,
автор: Nikolariys
Предмет: Информатика,
автор: sasha138906
Предмет: Математика,
автор: LarisaErmolaeva
Предмет: Математика,
автор: maximuchenik