Предмет: Геометрия,
автор: АртёмДолженЗнать
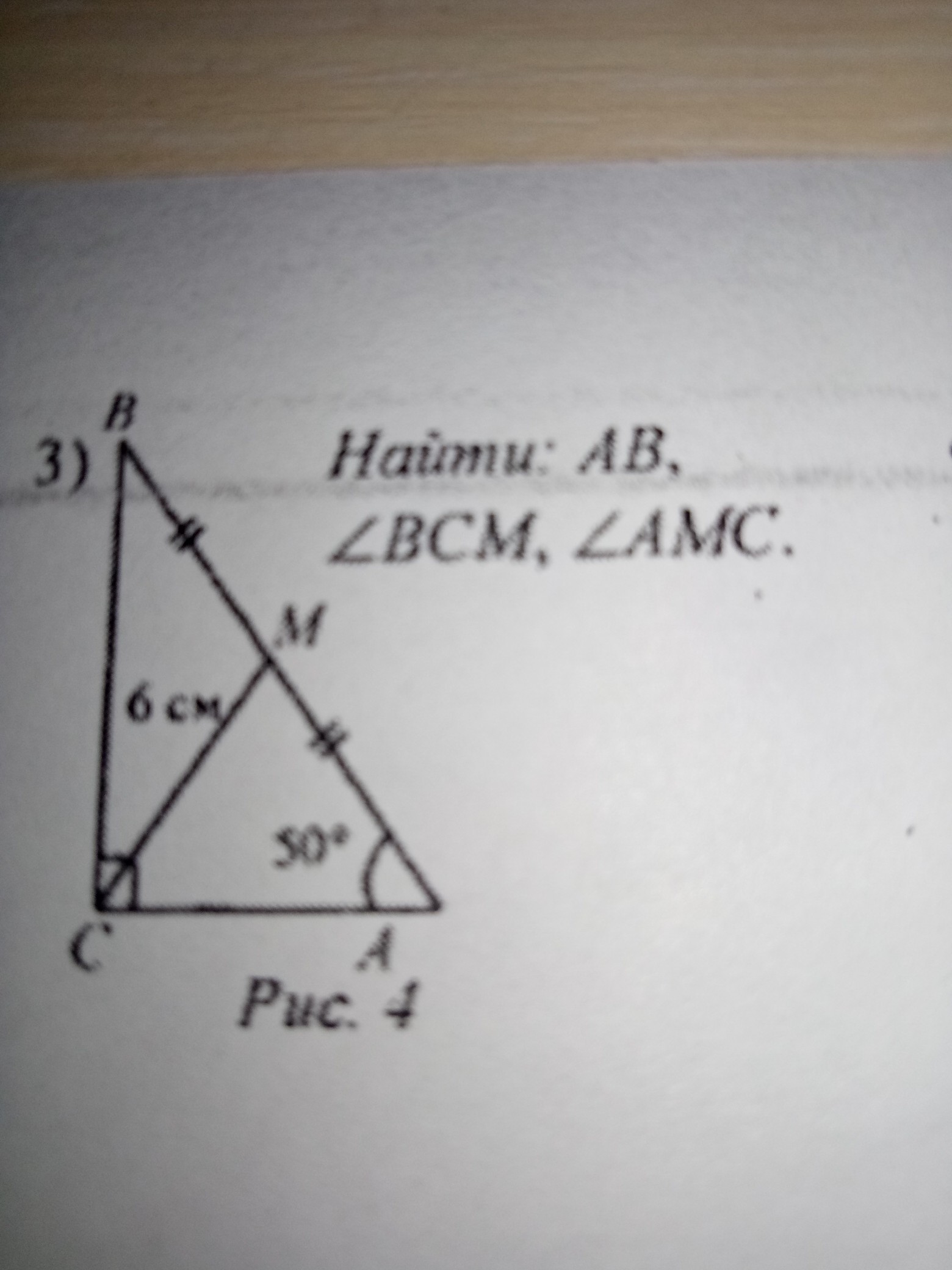
Найти АВ, ВСМ, АМС.
Приложения:
Ответы
Автор ответа:
7
BM = AM ⇒ CM - медиана
В прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы, т.е. гипотенуза больше медианы в 2 раза
AB = 2CM = 2*6 = 12 см
CM = AM = MB = 6 см
ΔABC - прямоугольный ⇒
∠B = 90° - ∠A = 90° - 50° = 40°
CM = BM ⇒ ΔCMB - равнобедренный ⇒
∠BCM = ∠B = 40°
∠AMC - внешний угол ΔCMB - равен сумме двух внутренних углов треугольника, не смежных с ним ⇒
∠AMC = ∠B + ∠BCM = 40° + 40° = 80°
Ответ: AB = 12 см; ∠BCM = 40°; ∠AMC = 80°
В прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы, т.е. гипотенуза больше медианы в 2 раза
AB = 2CM = 2*6 = 12 см
CM = AM = MB = 6 см
ΔABC - прямоугольный ⇒
∠B = 90° - ∠A = 90° - 50° = 40°
CM = BM ⇒ ΔCMB - равнобедренный ⇒
∠BCM = ∠B = 40°
∠AMC - внешний угол ΔCMB - равен сумме двух внутренних углов треугольника, не смежных с ним ⇒
∠AMC = ∠B + ∠BCM = 40° + 40° = 80°
Ответ: AB = 12 см; ∠BCM = 40°; ∠AMC = 80°
Похожие вопросы
Предмет: Математика,
автор: zivotnyeai
Предмет: Физика,
автор: hristinagac020
Предмет: Физика,
автор: meawirk
Предмет: Физика,
автор: lenslina