Предмет: Алгебра,
автор: 1un1happy
Решите неравенство, пожалуйста
Приложения:
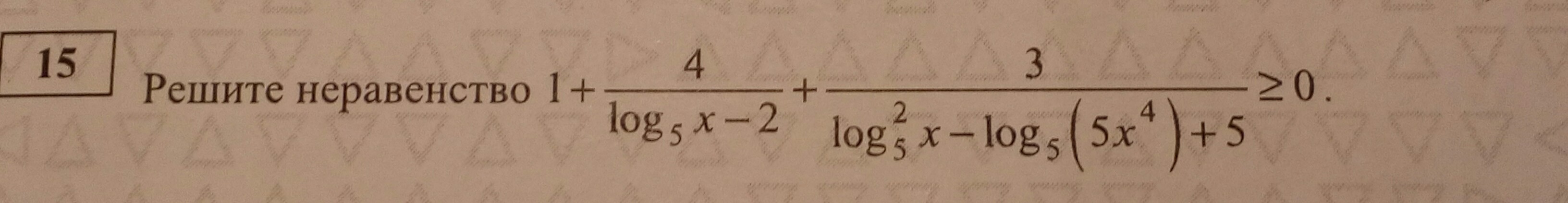
1un1happy:
А сейчас?
Ответы
Автор ответа:
0
начнём, пожалуй, с самого простого и интересного – области допустимых значений:
решим по отдельности каждое из уравнений системы, чтобы не мучиться с оформлением.
итак, решаем неравенство, учтя разложение на множители знаменателя второй дроби:
произведя замену
решаем неравенство относительно новой переменной:
произведя обратную замену, получаем, что:
решим отдельно совокупность неравенств, а затем пересечём их решения с ОДЗ:
ОТВЕТ:
Похожие вопросы
Предмет: Математика,
автор: lehaprcev2009
Предмет: Қазақ тiлi,
автор: abdakovalizan
Предмет: Геометрия,
автор: sofkoefkrat
Предмет: Математика,
автор: Nikita087