Предмет: Геометрия,
автор: СанекХений
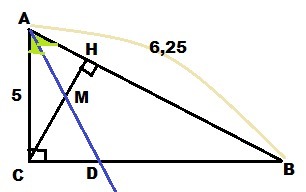
В прямоугольном треугольнике ABC с прямым углом C известно,что AB=6,25,AC=5.Найдите ,в каком отношении биссиктриса треугольника AD делит высоту CH.
Ответы
Автор ответа:
6
CH - высота прямоугольного треугольника ABC: ∠C = 90°
Высота CH, проведенная к гипотенузе AB, делит ΔABC на два подобных ΔACH ~ ΔCHB, которые подобны ΔABC ⇒
ΔACH ~ ΔABC ⇒

Биссектриса AM треугольника ΔACH делит противолежащую сторону CH пропорционально прилежащим сторонам AC и AH.

Ответ: CM:MH = 5:4
Высота CH, проведенная к гипотенузе AB, делит ΔABC на два подобных ΔACH ~ ΔCHB, которые подобны ΔABC ⇒
ΔACH ~ ΔABC ⇒
Биссектриса AM треугольника ΔACH делит противолежащую сторону CH пропорционально прилежащим сторонам AC и AH.
Ответ: CM:MH = 5:4
Приложения:
Похожие вопросы
Предмет: Физика,
автор: Taekookjktae
Предмет: Литература,
автор: gtatiana45
Предмет: Геометрия,
автор: kllopfty
Предмет: Обществознание,
автор: lidazaripowa