Question

вычислите координаты точек пересечения графиков функции y=4-x^2 и у=х-2

Answer 1

{y=4-x²

{y=x-2

x-2=4-x²

x²+x-6=0

D=1²-4*(-6)=1+24=25   √25=5

x₁=(-1+5)/2=2

x₂=(-1-5)/2=-3

y₁=2-2=0

y₂=-3-2=-5

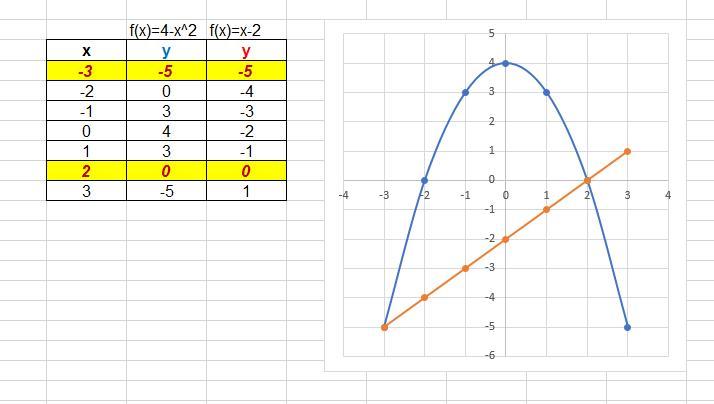
Точки пересечения графиков (2;0) и (-3;-5)

График во вложении

Answer 2

Ответ:

(-3; -5), (2;0)

Объяснение:

Найдем абсциссы точек пересечения , решив уравнение:

$4-x^{2} =x-2;\x^{2} +x-2-4=0;\x^{2} +x-6=0;\D= 1-4*(-6) =1+24=25>0,sqrt{D} =5;\left [ begin{array}{lcl} {{x=frac{-1-5}{2}, } \\ {x=frac{-1+5}{2}; }} end{array} right.Leftrightarrow left [ begin{array}{lcl} {{x=-3,} \ {x=2.}} end{array} right.$

Найдем ординаты точек пересечения

Если x= - 3, то y= - 3-2= - 5.

(-3; -5) - точка пересечения графиков.

Если x=2, то  y=2-2=0.

(2;0) -точка пересечения графиков.