Question

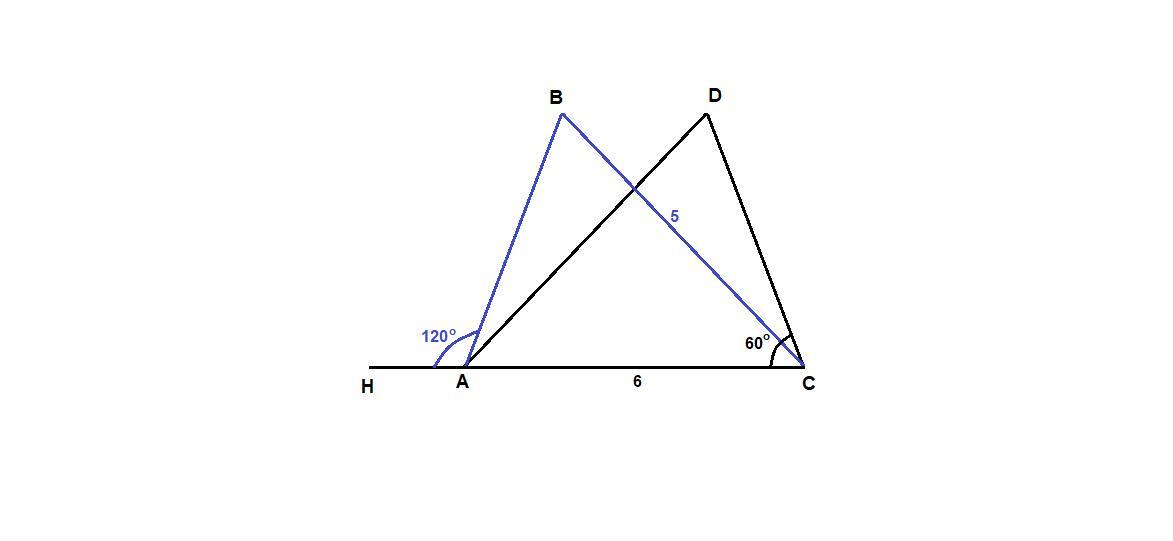
Периметр △ABC равен 18 см, сторона АС=6см, ВС=5см. Известно, что АВ=СD, ∠DCA=60°, ∠BAH=120°.  а) Докажите, что △АВС=△DCA.  б) Найдите длины сторон △DCA△.

Answer 1

Ответ:   5 см,    6 см,    7 см

Объяснение:

АВ = Pabc - (BC + AC) = 18 - (5 + 6) = 18  - 11 = 7 см

∠BAC = 180° - ∠DAH = 180° - 120° = 60° по свойству смежных углов,

АВ = CD по условию,

∠DCA = ∠ВАС = 60°,

АС - общая сторона для треугольников АВС и CDA, ⇒

ΔABC = ΔCDA по двум сторонам и углу между ними.

В равных треугольниках равны соответствующие стороны:

CD = АВ = 7 см

DA = ВС = 5 см

АС = 6 см