Предмет: Математика,
автор: alba132
найдите неопределенные интегралы,результаты проверить дифференцированием (под б)
Приложения:
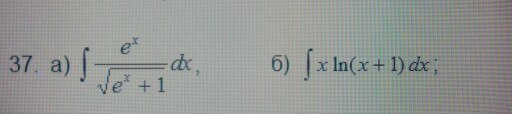
Ответы
Автор ответа:
0
Преобразуем подынтегральное выражение (можно и без этого, но мне показалось, что так проще).
Сначала возьмём второй интеграл (по частям):
Теперь первый интеграл (тоже по частям):
Собираем вместе, из первого вычитаем второй интеграл:
Проверяем дифференцированием:
Похожие вопросы
Предмет: Английский язык,
автор: yanalove0605
Предмет: География,
автор: mikhazakharov99
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: Модница333
Предмет: Алгебра,
автор: NikitaMarkov