Предмет: Алгебра,
автор: владсс
Помогите пожалуйста номера 15, 17 (б), 19
Приложения:
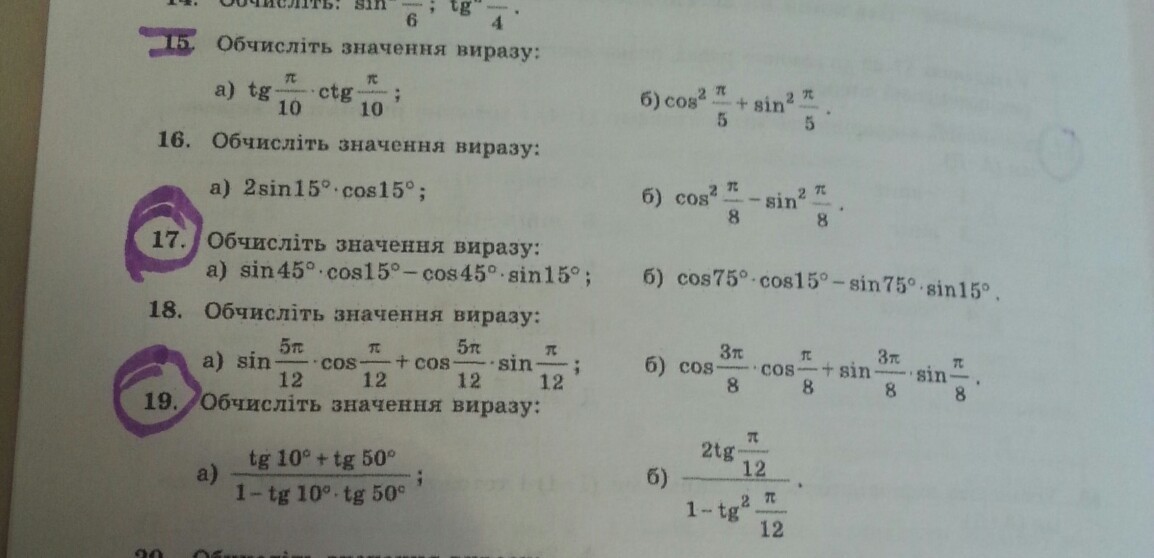
Ответы
Автор ответа:
0
15) tg(p / 10) * ctg(p / 10) = 1 так как:
tga*ctga=1
cos^2(p / 5) + sin^2(p / 5) = 1 так как:
sin^2a + cos^2a = 1
17)cos75*cos15-sin75*sin15=cos(75 + 15) = cos90 = 0
19) tg10 + tg50 / 1-tg10*tg50 = tg(50 + 10) = tg60 = √3
2tg(p / 12) / 1-tg^2(p / 12) = tg (2*(p /1 2)) = tg(p /6) = tg30 = 1/√3
tga*ctga=1
cos^2(p / 5) + sin^2(p / 5) = 1 так как:
sin^2a + cos^2a = 1
17)cos75*cos15-sin75*sin15=cos(75 + 15) = cos90 = 0
19) tg10 + tg50 / 1-tg10*tg50 = tg(50 + 10) = tg60 = √3
2tg(p / 12) / 1-tg^2(p / 12) = tg (2*(p /1 2)) = tg(p /6) = tg30 = 1/√3
drwnd:
там cos (75-15)
формула:Сos(a-b) = cosa*cosb + sina*sinb
cos(a+b)=cosa*cosb-sina*sinb
ш...точно, прошу прощения
Автор ответа:
0
15. Это вообще на знание основного тригонометрического тождества и из него вытекающих
а.

б.
 в данном случае это
в данном случае это 
ответ: 1
17. Это формулы сложения. Я не буду писать их все, но рекомендую посмотреть на досуге
а.
б.
19. Снова формулы сложения (в примере а) и формулы выражения тригонометрических функций через тангенс половинного угла (пример б):
a.
б.

а.
б.
ответ: 1
17. Это формулы сложения. Я не буду писать их все, но рекомендую посмотреть на досуге
а.
б.
19. Снова формулы сложения (в примере а) и формулы выражения тригонометрических функций через тангенс половинного угла (пример б):
a.
б.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Геометрия,
автор: evamyronenko
Предмет: Химия,
автор: zubenkou1978
Предмет: Русский язык,
автор: lizzzaxxs