Предмет: Математика,
автор: aleshenkastepa
Две бригады, работая вместе, могут вспахать поле за 3  часа. Работая порознь, первая бригада вспахивает поле на 4 часа быстрее второй. Найдите, за сколько часов может вспахать поле вторая бригада, работая самостоятельно.
часа. Работая порознь, первая бригада вспахивает поле на 4 часа быстрее второй. Найдите, за сколько часов может вспахать поле вторая бригада, работая самостоятельно.
Ответы
Автор ответа:
5
время, чтобы вспахать все поле первой бригаде х час
время, чтобы вспахать все поле 2 бригаде х+4 час
производительность ( или какая часть поля будет вспахана за 1 час)
1 бригады - 1/х
2 бригады- 1/(х+4)
Вместе за 1 час они вспашут 1/х+1/(х+4)
НА то чтобы вспахать все поле нужно 15/4 час
составим уравнение ( при условии, что все поле принимается за единицу)

Значит время первой бригады =6 час,
Второй бригады 6+4=10 час
чтобы вспахать все поле
время, чтобы вспахать все поле 2 бригаде х+4 час
производительность ( или какая часть поля будет вспахана за 1 час)
1 бригады - 1/х
2 бригады- 1/(х+4)
Вместе за 1 час они вспашут 1/х+1/(х+4)
НА то чтобы вспахать все поле нужно 15/4 час
составим уравнение ( при условии, что все поле принимается за единицу)
Значит время первой бригады =6 час,
Второй бригады 6+4=10 час
чтобы вспахать все поле
Автор ответа:
1
Решение задачи приложено
Приложения:
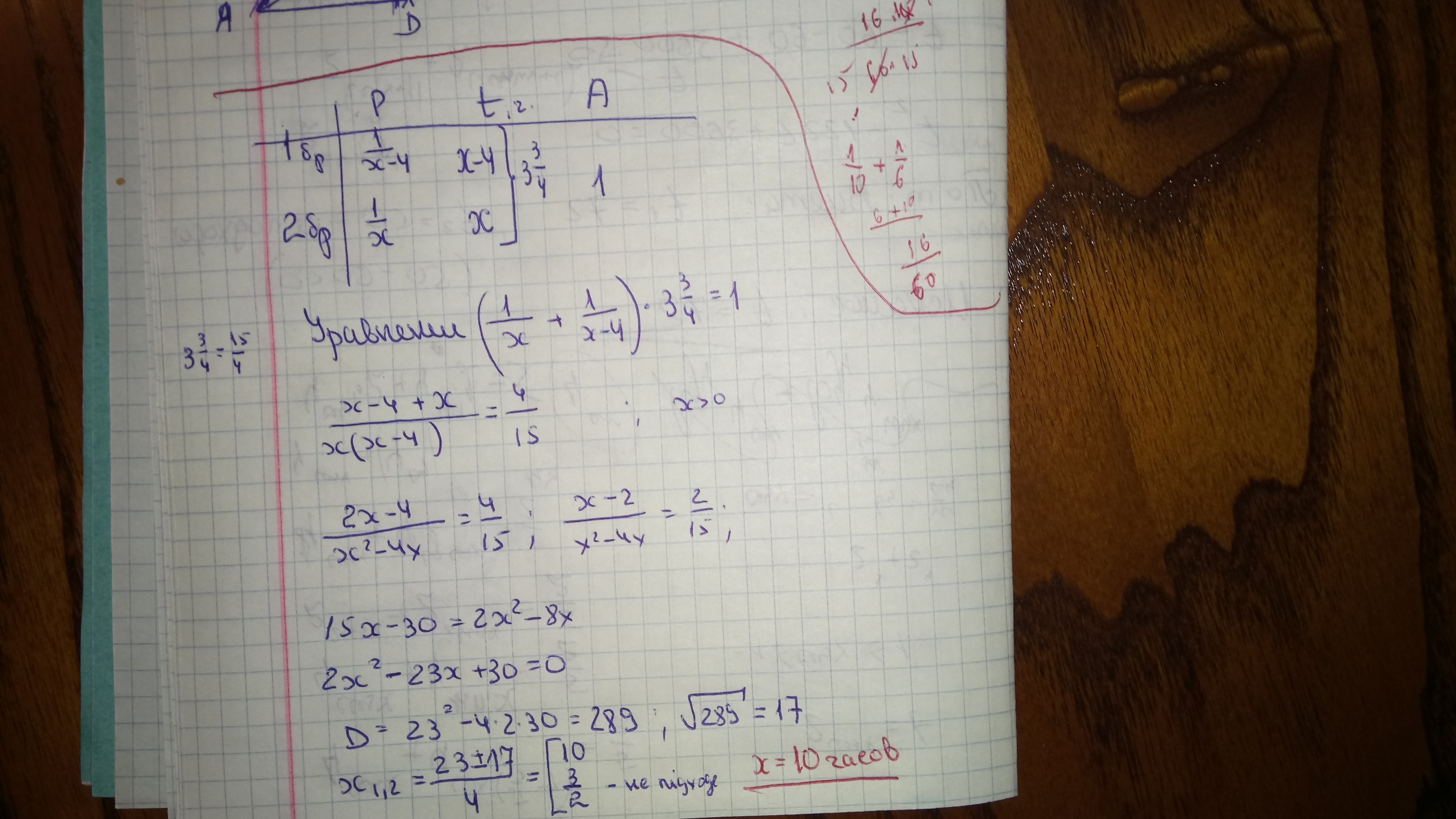
Похожие вопросы
Предмет: Физика,
автор: kotik766
Предмет: География,
автор: anitakrasova9
Предмет: История,
автор: solomiyagumeniuk
Предмет: Русский язык,
автор: tutsila
Предмет: Французский язык,
автор: bogolubovrom5