Предмет: Алгебра,
автор: Klender3055
1) у=((0,75х^(2)-0,75x) |х| ) / (х-1), построить график и определить, при каких значения m прямая y=m не имеет с графиком ни одной общей точки.
2) у=((0,25х^(2)+0,5x)|х|) / (х+2), построить график и определить, при каких значения m прямая y=m не имеет с графиком ни одной общей точки.
Ответы
Автор ответа:
0
1) При x < 0 будет |x| = -x, тогда

Так как x < 0, то x - 1 ≠ 0, и на него можно сократить
y = -0,75x^2
Это будет одна ветвь параболы, направленная вниз.
При любых m < 0 прямая y = m имеет 1 пересечение с этой ветвью.
Область определения D(X) = (-oo; 0), область значений E(Y) = (-oo; 0).
При x >= 0 будет |x| = x, тогда

Так как x >= 0, то может быть x = 1, поэтому сокращать нельзя.
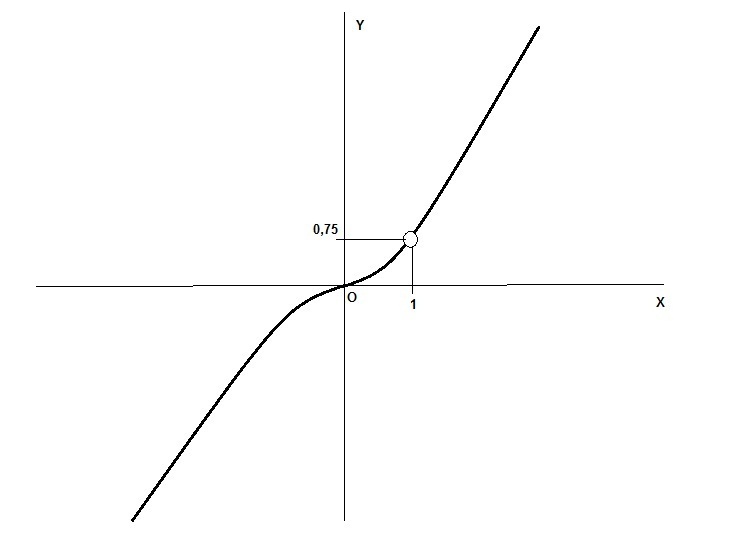
Это будет по сути парабола y = 0,75x^2, но с выколотой точкой M0(1; 0,75).
Одна ветвь параболы, направленная вверх.
При любом m ≠ 0,75 прямая y = m имеет 1 пересечение с этой ветвью.
И только при m = 0б75 пересечений графика прямой и параболы не будет.
Область определения D(X) = (0; 1) U (1; +oo).
Область значений E(Y) = (0; 0,75) U (0,75; +oo)
График на рисунке.
Ответ: m = 0,75
2) Точно такая же, я не буду подробно решать.

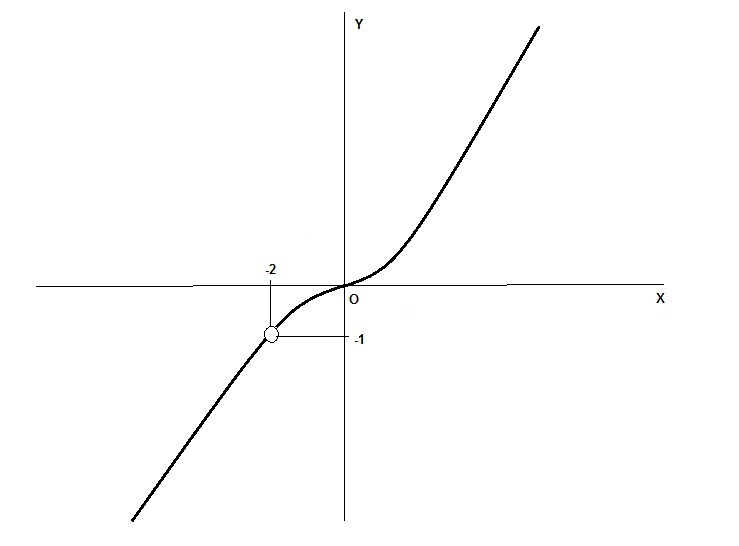
При x < 0 это ветвь вниз y = -0,25x^2 с выколотой точкой M0(-2; -1)
При x > 0 это ветвь вверх y = 0,25x^2 без выколотых точек.
График на 2 рисунке
Ответ: m = -1
Так как x < 0, то x - 1 ≠ 0, и на него можно сократить
y = -0,75x^2
Это будет одна ветвь параболы, направленная вниз.
При любых m < 0 прямая y = m имеет 1 пересечение с этой ветвью.
Область определения D(X) = (-oo; 0), область значений E(Y) = (-oo; 0).
При x >= 0 будет |x| = x, тогда
Так как x >= 0, то может быть x = 1, поэтому сокращать нельзя.
Это будет по сути парабола y = 0,75x^2, но с выколотой точкой M0(1; 0,75).
Одна ветвь параболы, направленная вверх.
При любом m ≠ 0,75 прямая y = m имеет 1 пересечение с этой ветвью.
И только при m = 0б75 пересечений графика прямой и параболы не будет.
Область определения D(X) = (0; 1) U (1; +oo).
Область значений E(Y) = (0; 0,75) U (0,75; +oo)
График на рисунке.
Ответ: m = 0,75
2) Точно такая же, я не буду подробно решать.
При x < 0 это ветвь вниз y = -0,25x^2 с выколотой точкой M0(-2; -1)
При x > 0 это ветвь вверх y = 0,25x^2 без выколотых точек.
График на 2 рисунке
Ответ: m = -1
Приложения:
Похожие вопросы