Question

Острый угол B прямоугольного треугольника ABC равен 65 градусов найти угол между высотой и медианой

Answer 1

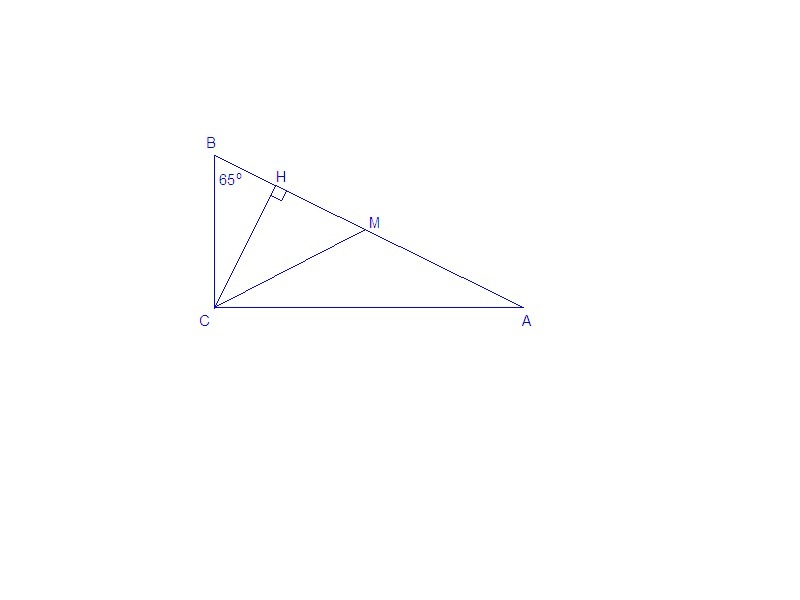
СМ - медиана, СН - высота прямоугольного треугольника АВС.

∠НСМ - искомый.

Сумма острых углов прямоугольного треугольника равна 90°.

ΔВСН: ∠ВНС = 90°, ∠НВС = 65°, ⇒ ∠ВСН = 90° - 65° = 25°.

ΔАВС: ∠АСВ = 90°, ∠АВС = 65°, ⇒ ∠ВАС = 90° - 65° = 25°.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине:

СМ = АМ = ВМ,

значит ΔСАМ равнобедренный, углы при основании равны:

∠МСА = ∠МАС = 25°.

∠НСМ = ∠АСВ - ∠ВСН - ∠МСА = 90° - 25° - 25° = 40°