Question

10 баллов! ПОЖАЛУЙСТА. ОЧЕНЬ НАДО.
2cos³x+cos(п-x)=0 надо решить 4-мя способами. отбор корней по единичной окр-ти, перебором значений, аналитически с помощью неравенств и по графику.

Answer 1

$2cos^3x+cos(pi-x)=0\2cos^3x-cos x=0\cos x(2cos^2x-1)=0\ begin{cases}cos x=0\2cos^2x-1=0end{cases}Rightarrowbegin{cases}cos x=0\cos x=pmfrac1{sqrt2}end{cases}Rightarrowbegin{cases}x=fracpi2+pi n\x=pmfracpi4+2pi n\x=pmfrac{3pi}4+2pi nend{cases}\;ninmathbb{Z}$
1. Круг в приложении. Второй и третий корни можно объединить в один, первый остаётся без изменений:
$x_1=fracpi2+pi n\x_1=fracpi4+fracpi2n$
2. Перебор значений целочисленного параметра n производится тогда, когда задан отрезок, которому должны принадлежать корни. В задании отрезок не указан.
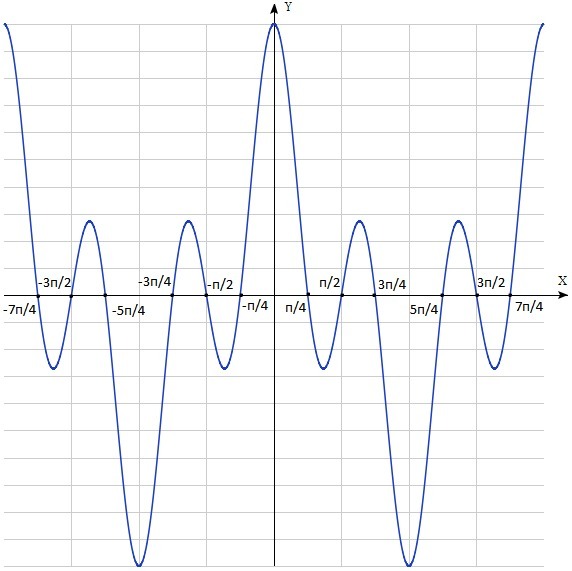
3. График в приложении.