Предмет: Геометрия,
автор: mashka9aklass
Найдите площадь прямоугольной трапеции боковые стороны которой равны 12см и 13 см, а основания относятся как 4:9
Ответы
Автор ответа:
0
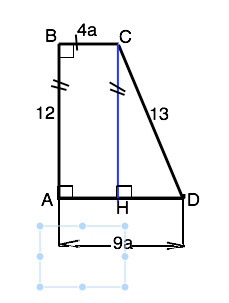
Обозначим трапецию АВСD, угол А=В=90°. Пусть ВС=4а, тогда АD=9а.
Опустим из вершины С высоту СН. Четырехугольник АВСН - прямоугольник, поэтому АН=ВС, СН=АВ=12 см. По т.Пифагора НD=√(CD²-CН²)=√(13²-12²)=5 см. ⇒ АD=ВС+5; 9а=4а+5, откуда а=4 см. Площадь трапеции равна произведению высоты на полусумму оснований. S=12•(4+9):2=78см*
Приложения:
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: rozanurahmetova55
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: Lida56
Предмет: Геометрия,
автор: KKKKKKK777