Предмет: Алгебра,
автор: kolupaeva1234
помогите пожалуйста)))доказать неравенство
Приложения:
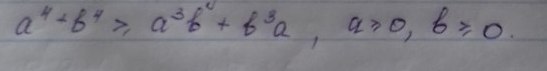
Ответы
Автор ответа:
0
1) перенесём всё в левую часть
2) вынесем a³ и b³
3) (b-a)=-(a-b)
4) выносим (a-b)
5) применим формулу разности кубов( a³-b³=(a-b)(a²+ab+b²) )

Рассмотрим 2 множителя.
(a-b)² - число неотрицательное(≥0), т.к. возводим в чётную степень
a²+ab+b² - также неотрицательное, т.к. сумма неотрицательных чисел(a² и b², т.к. чётная степень; ab - т.к. произведение неотрицательных(по условию) чисел неотрицательно).
И тут получаем произведение неотрицательных чисел, которое ≥0. Неравенство доказано.
2) вынесем a³ и b³
3) (b-a)=-(a-b)
4) выносим (a-b)
5) применим формулу разности кубов( a³-b³=(a-b)(a²+ab+b²) )
Рассмотрим 2 множителя.
(a-b)² - число неотрицательное(≥0), т.к. возводим в чётную степень
a²+ab+b² - также неотрицательное, т.к. сумма неотрицательных чисел(a² и b², т.к. чётная степень; ab - т.к. произведение неотрицательных(по условию) чисел неотрицательно).
И тут получаем произведение неотрицательных чисел, которое ≥0. Неравенство доказано.
Похожие вопросы
Предмет: География,
автор: vladoche4ka
Предмет: Математика,
автор: azimakay37
Предмет: Английский язык,
автор: 09988665557hhg
Предмет: Алгебра,
автор: DashaKalinina1
Предмет: Математика,
автор: katya272015