Question

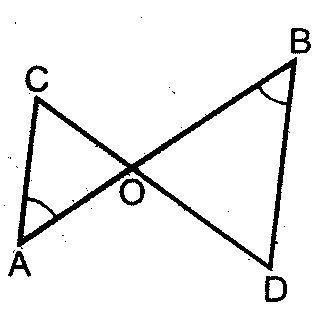
Дано: угол А=угол В,СО=4,DO=6,AO=5
Найти:
а)OB; АС:ВD;SAOC:SBOD
Рисунок к задаче в приложении.

Answer 1

Равные по условию ∠А и ∠В- накрестлежащие при пересечении двух прямых секущей АВ⇒

АС║BD. 

Углы при О равны как вертикальные. 

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

∆ АСО и ∆ ВDО подобны по первому признаку подобия треугольников. 

Из подобия следует отношение:

СО:OD=AO:OB

4:6=5:ОВ⇒

ОВ=30:4=7,5

Коэффициент подобия равен отношению сходственных сторон. 

k=СО:OD= 4/6=2/3⇒

АС:ВD=2/3

Отношение площадей подобных треугольников равно квадрату коэффициента их подобия:

SAOC:SBOD =k²=(2/3)²=4/9